https://dl.acm.org/doi/pdf/10.1145/3654920
Keywords: Missing Data Imputation, Neural Network Gaussian Process
데이터셋의 완전성을 달성하기 위해 누락된 데이터를 대치하는 것을 목표로 하는 데이터 품질 영역의 기본 작업인 누락 데이터 대체 문제를 연구한다. 비록 최근의 분포 모델링 기반 기술 (분포 생성 및 분포 매칭)은 대치 정확도 측면에서 최첨단 성능을 달성할 수 있지만, (1) 누락된 데이터 대체에 과적합되는 경향이 있는 정교한 딥러닝 모델을 배포하는 점과 (2) 지역정보(local information)을 간과하면서 전역정보 (global information) 에 직접적으로 의존한다는 점을 주목한다.
누락된 데이터와 누락된 메커니즘의 고유한 가변성에 힘입어 이 논문에서 우리는 이 작업의 불확실한 성격을 탐구하고 uNcertainty-driven network for Missing Imputation (NOMI) 라고 불리는 누락된 데이터 대체를 위한 불확실성 기반의 네트워크를 제안하여 기존 작업이 한계를 해결하는 것을 목표로 한다.
NOMI는 세가지 주요한 구성 요소가 있다. (1) retrieval module, (2) the neural network gaussian processs imputator(NNGPI), (3) the uncertainty-based calibration module. NOMI는 더 나은 성능을 달성하기 위해 이러한 구성 요소들을 순차적으로 반복적인 방식으로 실행한다.
(1) Retrieval module: NOMI는 사전 정의된 유사성 메트릭을 기반으로 불완전한 데이터 샘플의 로컬 이웃을 검색한다.
(2) NNGPI: Gaussian Process의 장점과 신경망의 보편적인 근사 능력을 결합, 과적합 문제를 완화하면서 누락된 값을 대치하기 위해 데이터에 대한 사후 분포를 학습하여 불확실성을 모델링한다.
또한, 추론 모듈이 보다 신뢰할 수 있는 로컬 정보를 얻을 수 있도록 추론자의 불확실성을 예측에 활용하는 불확실성 기반 보정 모듈을 제안하여 추론 성능을 더욱 향상시킨다. 또한, 잘 알려진 Expectation Maximization(EM) 알고리즘의 인스턴스로 NOMI를 재구성할 수 있음을 보여줌으로써 제안된 방법의 강력한 이론적 토대를 강조한다. 12개의 실제 데이터 세트에 대한 실험이 수행되었고, 그 결과 정확도와 효율성 측면에서 NOMI의 뛰어난 성능이 입증되었다.
Introduction
데이터 수집 품질 저하, 개인정보 보호 문제 등 다양한 이유로 인해 많은 애플리케이션에서 누락된 데이터 문제가 발생하고 있다. 다양한 데이터 분석 작업에서 데이터의 완전성(completeness) 이 매우 중요하다는 것은 잘 알려져 있다. 예를 들어, 대부분의 딥러닝 모델과 알고리즘은 데이터로부터 의사 결정을 학습하는 데이터 기반이다. 따라서 모델이 garbage in, garbage out (GIGO) 증후군의 희생양이 되는 것을 방지하기 위해 데이터 품질에 대한 연구가 광범위하게 이루어지고 있다. 원본 데이터 세트에서 누락된 데이터를 적절히 처리하기 위해, 데이터의 완전성을 달성하기 위해 관찰된 데이터 샘플과 특징의 정보를 사용하여 누락된 값을 예측하는 누락 데이터 대입이 제안되었다.
(Exisiting Solutions) 누락 데이터 대입 문제에 대한 연구는 오랜 역사를 가지고 있다. 초기에는 통계 기반 대치 방법과 유사도 기반 방법이 간단하고 직관적인 방법으로 제안되었다. 그러나 단순 대체나 집계는 데이터를 정확하게 맞출 수 있는 기능이 부족 하기 때문에 성능이 기대 이하로 떨어진다. 데이터를 더 잘 모델링하기 위해 일부 전통적인 머신 러닝 방법이 이 작업에 적용되어 압축 기반 방법 (Compression-based method) 과 회귀 기반 방법으로 이어졌다.
압축 기반 방법은 먼저 데이터 행렬을 분해한 다음 재구성한다. 하지만 분해 과정은 시간이 오래 소요된다. 또한 이러한 방법은 선형성 가정에 의존하기 때문에 데이터의 복잡한 관계나 패턴을 포착하지 못할 수도 있다. 회귀 기반 대입 방법은 관찰된 특징과 누락된 특징 사이의 관계를 모델링하는 것을 목표로 한다. 그러나 일부 특징들 간의 약한 상관관계는 회귀 기반 대입 방법에 문제를 야기한다.
최근 이 분야에서는 분포 모델링 기법을 통한 결측 데이터의 대입에 초점을 맞춘 유망한 연구 동향이 나타나고 있다. 이러한 연구 방향은 기본 데이터 분포를 파악하는 학습을 추구하며, 크게 (1) 분포 생성 기반 추정 방법과 (2) 분포 매칭 기반 추정 방법으로 나뉜다.
(1) 분포 생성 기반 대체 방법은 VGAIN이 대표적인데, 자동 인코더(AE)와 생성적 적대 신경망(GAN) 같은 심층 생성 모델을 적용하여 데이터의 전역 분 포를 학습한다. 그런 다음 조작된 데이터가 학습된 분포에 잘 맞도록 누락된 데이터를 추론하여 누락 데이터 추론 성능이 우수하도록 한다.
(2) TDM이 대표적인 분포 매칭 기반 추정 방법은 원본 데이터 세트의 두 데이터 배치는 동일한 전역 분포에서 비롯되며 해당 분포 는 원본 데이터 공간 또는 잠재 공간에서 일치해야 한다는 아이디어를 포착한다. 따라서 누락된 데이터를 추정하기 위해 신경망을 사용하여 추정된 데이터 배치의 경험적 분포 사이의 Optimal Transport distance가 최소화되도록 한다.
(Motivations) VGAIN과 TDM은 정확도 측면에서 인상적인 성능을 보여주었지만, 두 가지 주요 한계가 남아 있다.
첫째, 이러한 분포 모델링 기반 접근법은 정교한 딥러닝 모델을 배포하므로, 특히 누락 데이터 대입 작업에서 과적합의 위험이 내재적으로 존재한다. 누락된 데이터 대입을 위해 딥러닝 모델을 학습할 때 학습된 모델에는 학습 데이터의 복잡한 패턴을 포착할 수 있는 많은 수의 매개변수가 포함될 수 있다. 그러나 이로 인해 모델이 새로운 테스트 데이터로 잘 일반화하도록 학습하기보다는 단순히 훈련 데이터를 암기하게 되어 부정확한 대치가 발생할 수 있다. 또한 데이터 누락 메커니즘이 구조화되지 않은 경우 모델은 학습 데이터에 존재하는 특정 누락 메커니즘을 과도하게 적합화하여 다양한 누락 시나리오에 적응하는 데 어려움을 겪을 수 있다.
둘째, 이러한 분포 모델링 기반 접근 방식은 누락된 데이터를 추정하기 위해 글로벌 분포에 크게 의존하는 반면, 로컬 정보는 충분히 탐색되지 않는다. 즉, 학습 샘플에서 얻은 기본 글로벌 분포에 따라 누락된 값을 추정한다. 그러나 하나의 데이터 세트 내의 데이터 샘플은 다양한 출처에서 가져올 수 있으며, 글로벌 분포는 개별 샘플 간의 차이와 고유성을 로컬에서 간과하는 경향이 있다. 이러한 로컬 정보는 일반적으로 글로벌 분포 내의 특정 하위 집합이나 로컬에 대한 가치있는 컨텍스트를 제공하여 보다 세밀하고 정확한 대치를 가능하게 한다.
(Challenges) 효과적인 대치 방법을 설계하려면 다음과 같은 두 가지 주요 어려움이 있다.
Challenge 1: How to design an effective and efficient imputator that can alleviate the overfitting problem?
누락된 데이터와 누락된 메커니즘의 다면적인 특성은 과적합 문제를 복잡하게 만든다. 과적합 문제를 완화하는 간단한 방법 중 하나는 정규화 기법을 사용하는 것이다. 그러나 이러한 정규화 기법은 복잡한 관계를 처리하기 어렵다. 또 다른 유망한 방향은 Bayesian Deep Learning (BDL) 모델을 활용하는 것입니다. BDL 방법은 파라미터의 불확실성을 모델링하고 과적합 문제를 완화하는 데 효과적인 사후 분포를 학습한다. 그러나 기존 BDL은 사전 분포를 지정해야 하므로 모델의 성능과 유연성이 제한된다. 또한 기존 BDL은 샘플링 방법 (eg. Markov Chain Monte Carlo)을 사용하여 사후 분포를 근사화하는데, 이는 시간이 많이 소요되는 프로세스이다. 따라서 과적합 문제를 완화하면서 효율적이고 효과적으로 누락된 데이터를 추정하는 방법은 어려운 문제이다.
Challenge 2: How to find reliable local information in the context of missing data?
누락된 데이터가 있으면 로컬 정보 검색의 복잡성이 증가한다. 로컬 정보를 얻는 간단한 방법 중 하나는 유사도 기반 방법 및 K-Nearest Neighbor (KNN)를 직접 사용하는 것이다. 그러나 누락된 데이터가 존재하면 가장 가까운 이웃 검색이 부정확해진다. 또 다른 고급 접근 방식은 대입 후 KNN 검색을 여러 번 반복하는 것이다. 그러나 편차가 큰 대치의 경우 반복할 때마다 오차가 전파되고 누적될 수 있다. 따라서 데이터가 누락된 상황에서 신뢰할 수 있는 로컬 정보를 찾는 것은 어려운 일이다.
(Solutions) 누락 데이터와 누락 메커니즘의 본질적인 가변성으로 인해 누락 데이터 추정에 불확실성이 만연해 있음을 관찰했다. 앞서 언급한 문제와 누락 데이터 추정의 불확실한 특성에 기반하여, uNcertainty-driven netwOrk for Missing data Imputation (NOMI)를 제안한다. NOMI는 (1) 검색 모듈, (2) Neural Network Gaussian Process Imputator (NNGPI), (3) 불확실성 기반 보정 모듈이라는 세 가지 핵심 구성 요소를 반복적인 방식으로 실행한다. 이러한 구성 요소는 서로 연결되어 있으며, NNGPI가 추정하는 예측과 불확실성은 불확실성 기반 보정 및 검색 모듈이 보다 정확하고 신뢰할 수 있는 로컬 정보를 식별하는 데 도움을 준다. 결과적으로 신뢰할 수 있는 로컬 정보는 NNGPI의 대치 성능을 향상시킨다.
(1) Neural Network Gaussian Process Imputator (NNGPI).
신경망 가우스 프로세스를 기반으로 하는 NNGPI를 고안하여 challenge 1을 해결했다. NNGPI는 숨겨진 계층에 무한한 수의 뉴런을 가지고 있으며 가우시안 프로세스(GP)와 동등한 성능을 발휘한다. NNGPI는 GP처럼 작동함으로써 불확실성을 정량화하고 다양한 타당성 함수를 고려하여 확률적으로 예측함으로써 특정 예측에 대한 과신을 피함으로써 과적합을 완화한다. NNGPI는 GP의 유리한 특성을 유지하는 것 외에도 신경망의 보편적인 근사화 기능도 보유하고 있다. 신경망의 표현 학습 기능을 활용함으로써 NNGPI는 데이터의 복잡한 패턴과 구조를 효과적으로 포착한다. 기존의 BDL 모델과 달리, NNGPI는 신경망을 활용해 복잡한 함수를 근사화하므로 사전 분포에 대한 특정 매개변수 형식 없이도 다양한 데이터 분포에 유연하게 적응할 수 있다. 또한, NNGPI에 분석 솔루션이 포함되어 있어 기존 BDL 모델에 비해 효율적인 계산과 빠른 학습이 가능합니다.
(2) 검색 모듈 및 불확실성 기반 보정.
신뢰할 수 있고 정확한 지역 정보를 찾기 위해 검색 모듈 외에 불확실성 기반 보정 기법을 도입했다. 좀 더 구체적으로 설명하자면, (1) 학습된 불확실성, (2) 현재 반복 에서 예측된 값, (3) 이전 반복에서 예측된 값을 고려하여 데이터 세트를 보정하는 데 NNGPI의 출력을 활용한다. 보정은 불확실성이 낮으면 현재 반복의 예측에 우선순위를 두고, 불확실성이 높으면 이전 반복의 예측에 우선순위를 둔다. 이러한 방식으로 NOMI는 높은 수준의 신뢰도로 데이터 세트를 업데이트하여 로컬 정보를 얻을 때 발생하는 대치 오류 누적 문제를 완화할 수 있다.
검색 모듈에서는 미리 정의된 메트릭 (e.g. L2 distance) 을 기반으로 가장 가까운 상위 이웃을 검색하여 로컬 정보를 캡처한다. 그런 다음 NOMI는 검색 모듈, NNGPI 및 불확실성 기반 데이터 보정 기술을 여러 차례 반복하여 순차적으로 적용함으로써 NNGPI 단계와 로컬 정보 검색 단계 간의 상호 유익한 관계를 촉진하여 전반적인 대치 성능을 향상시킨다. 또한, NOMI 프레임워크가 EM 알고리즘의 인스턴스로 자연스럽게 해석될 수 있음을 보여준다. 이러한 대응은 NOMI와 잘 확립된 EM 알고리즘 사이의 연관성을 강조하며, 이를 통해 NOMI는 점진적으로 개선되는 NNGPI의 추론 정확도와 같은 EM 알고리즘의 바람직한 특성을 상속할 수 있게 됩니다.
Contributions.
- 누락된 데이터 대입의 성능을 크게 향상시키기 위해 새로운 프레임워크인 NOMI를 제안한다. 이 프레임워크는 일련의 반복적인 단계를 통해 검색 모듈, NNGPI 및 불확실성 기반 데이터 보정 기능을 결합한다.
- 불확실성 모델링에 기반한 효과적이고 효율적인 대입 기법인 NNGPI를 설계했다. 신경망의 강력한 근사화 기능과 가우시안 프로세스의 바람직한 특성을 결합한 기법이다.
- 보다 신뢰할 수 있는 지역 정보를 찾기 위해 불확실성 기반 보정 모듈과 검색 모듈을 고안합니다. 학습된 불확실성은 다양한 반복을 통해 예측의 균형을 효과적으로 맞추기 위해 활용된다.
- NOMI 프레임워크가 EM 알고리즘의 관점에서 이해될 수 있음을 보여줌으로써 EM 알고리즘에서 물려받은 NOMI의 이론적 기반과 좋은 속성을 강조한다.
Preliminaries

(Problem Statement) 결측치 대치 작업은 데이터 행렬 X 에서 관찰되지 않은 요소 (i.e. 마스크 행렬 M에서 mi,j가 0인 부분) 대치하고 만약 실제 완전한 데이터셋이 존재한다면 최대한 가깝게 만드는 것을 목표로 한다.
VGAIN
VGAIN은 훈련 데이터의 잠재 분포를 학습하기 위해 Generator와 Discriminator 두 가지 구성 요소를 사용한다.
구체적으로 데이터 행렬 X, 마스크 행렬 M, 그리고 노이즈 행렬 Z가 입력으로 주어지면, Generator는 다음과 식과 같이 학습된 분포에 따라 대치된 행렬을 출력으로 준다.
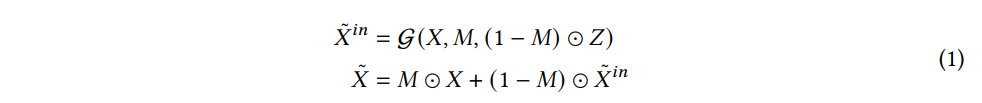
Discriminator는 추정된 데이터가 생성된 것인지 아니면 원래 분포에서 나온 것인지 판별하도록 설계되었다. 판별자는 다음과 같이 구성되어 있다.
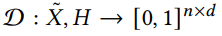
where D(˜X,H)i,j is the probability that the j-th component of ˜xi is observed and H is the hint matrix which contains a fraction of the mask matrix.
이 모델은 마스크 행렬 M을 정확하게 얘측할 확률을 최대화하도록 훈련되는 동시에 M을 예측할 확률을 최소화하도록 훈련되는 적대적 방식 (adversarial manner) 으로 훈련된다. Reconstruction loss도 훈련을 위해 통합된다.
TDM
TDM은 X1 과 X2 두 개의 데이터 배치를 추정된 데이터의 경험적 분포가 잠재공간에서 일치하도록 대치하는 것을 목표로 한다. 이를 위해 다음과 같은 목적함수를 고려한다.
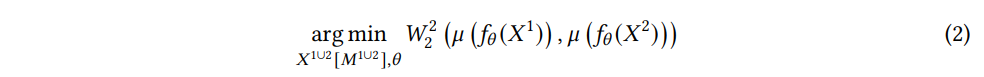
where μ(X1) denotes the empirical measure associated to the samples in X1 . X^{1\cup2} is the union of X1 and X2 , i.e., the unique data samples of the two batches. fθ(⋅) is a deep transformation layer that projects the data to the latent space. And W22(⋅) is the 2-Wasserstein distance to measure the distance between two distributions.
두 접근 방식 모두 복잡한 딥러닝 모델을 활용하므로 결과적으로 과적합의 잠재적 위험이 있다. 또한, 이러한 방법은 학습 데이터셋에서 학습한 글로벌 데이터 분포에 크게 의존하는 반면 로컬 정보는 충분히 탐색하지 못한다. 이러한 한계로 인해 누락 데이터 대치의 성능을 향상 시키기 위해 NOMI를 설계하게 되었다.
Methodology
(1) Retrieval and Input Construction
Nearest Neighbor search 방법을 이용하여 로컬 정보를 검색한다. 이 방법은 주어진 유사도 메트릭 (여기서는 L2 distance) 을 기준으로 입력 쿼리 샘플과 학습 데이터셋의 각 데이터 샘플 간 쌍별 유사성을 계산한다.
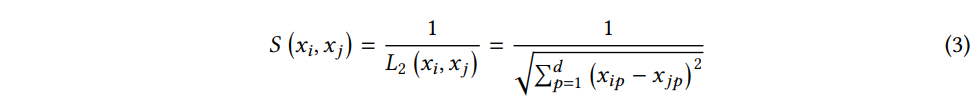
그런 다음 유사도 점수가 가장 높은 top-K 개를 선택하여 neighbor set N(xi) 을 구성한다. (n(N(xi))=K)
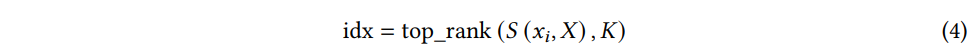
where top_rank(⋅,K) selects the index of the sample with its corresponding similarity score being the top-K highest w.r.t the query.
그런 다음 로컬 정보에 의해 증강되는 입력은 다음과 같이 구성된다.
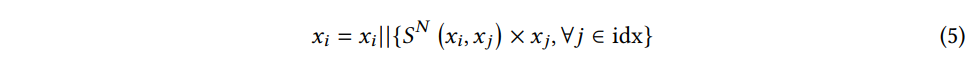
where SN(xi,xj) is the normalized value of S(xi,xj), and || indicates the concatenation operation.
증강 과정은 훈련 샘플과 테스트 샘플 모두 수행된다. 유사성을 가중치 요소로 통합함으로써 가까운 이웃에 더 높은 가중치를 적응적으로 할당하여 보다 효과적이고 포괄적인 지역 정보를 캡쳐할 수 있다.
검색 단계는 approximate K nearest neighbor (AKNN) 검색을 위한 효율적인 알고리즘인 HNSW로 구현한다. 정확한 nearest neighbor search 알고리즘과 비교할 때, HNSW의 AKNN은 훨씬 더 효율적이고 경쟁력 있는 정확도를 가지고 있다.
(2) Neural Network Gaussian Process Imputator (NNGPI)
(Traditional Deep Learning) 딥러닝에서 모델은 완전 연결 계층 (fully connected layer), 컨볼루션 계층, ReLU 등 다양한 신경망 계층으로 구성된다. 다양한 계층의 스택과 역전파의 이점을 활용하여 이 모델을 사용하면 , 함수 fw(x) 를 입력 x와 타겟 t 사이에 w로 파라미터화한다. 훈련 데이터 x∈X 가 주어지면, 모델은 다음과 같은 예측된 결과와 타겟 사이의 목적함수 L(fw(x),t) 를 최적화하기 위해 학습한다. 모델이 수렴할 때, 매개변수 w는 다음과 같은 식에 의해 결정된다.
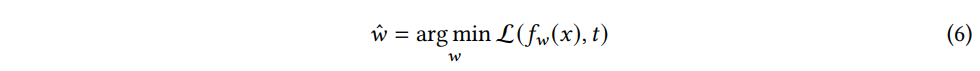
추론 과정에서 일반적인 신경망은 다음과 같이 모델 추론을 통해 결정론적(deterministic) 으로 타겟을 추정한다.
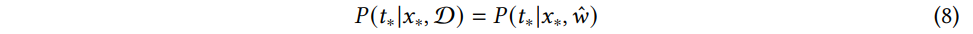
(Bayesian Deep Learning) 반면 베이지안 딥러닝은 신경망의 파라미터를 확률변수로 취급한다. 신경망의 파라미터 w는 결정론적이지 않고 사전 분포 P(w) 에서 샘플링되며, 분포는 marginalization 함으로써 학습된다. 훈련 데이터셋 D=(X,T) 이 주어지면, 베이지안 딥러닝은 p(w|X,T) (w의 사후 확률) 을 학습한다.
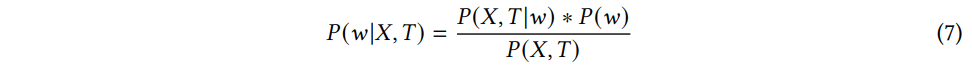
where P(X,T|w) is the likelihood probability of X, T given the weight w, P(w) is the prior probability of the weight w, and P(X,T) is marginal probability of training dataset X, T.
반면에 베이지안 딥러닝 모델은 추론과정에서 사후 확률의 합으로 주어진 테스트 데이터 x∗ 에 대한 예측 분포 P(t∗|x∗,ˆw) 를 추정한다.
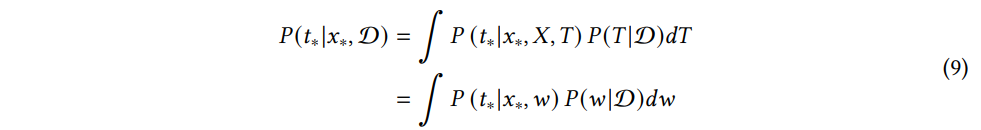
베이지안 딥러닝은 모든 잠재적 가중치로 파라미터화된 신경망의 출력을 합성하여 예측을 내리는데, 각 출력은 파라미터 w 의 사후분포 P(w|D) 에 의해 가중치가 부여된다. 이 사후분포는 관측된 데이터가 주어졌을 때 모델 파라미터에 대한 갱신된 지식을 나타낸다. 베이지안 딥러닝으로 학습한 사후분포는 확률 분포이므로 모델 매개변수에 대한 불확실성의 척도를 제공할 수 있다. 모델 매개변수의 불확실성을 고려함으로써 베이지안 딥러닝은 모델 예측의 불확실성도 추정할 수 있다.
(Gaussian Process) Stochastic Process 는 주어진 입력 데이터셋 X 에 대한 확률변수들 g(x)|x∈X 의 집합이다.

Gaussian Process 의 정의를 살펴보면, g(x)의 기댓값을 나타내는 평균함수 μ(x) 와 공분산 함수 K(x)i,xj) 로 정의할 수 있는 랜덤 프로세스이다. 더해서, 유한한 변수들의 집합 g(xi)ki=1 는 결합 다변량 정규분포를 따른다.
훈련 데이터 X=x1,⋯,xn (xi∈Rd0) 가 주어지면 관측된 데이터에 적용된 GP 모델에 대한 기본 가정은 사전 확률적 프로세스에서 생성된 후 독립 가우시안 노이즈가 추가된다는 가정이다.
Example) ρ0 개의 basic function f(⋅) 을 가지고, 출력이 g(x) 인 단순 선형 모델을 고려해보자
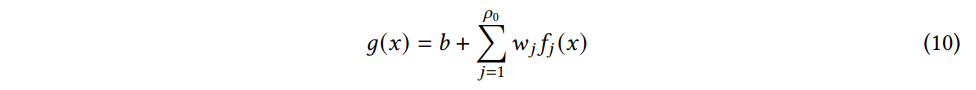
where w and b are the weight and bias of the basic functions, respectively.
가우시안 사전 분포는 w∼N(0,σ2wI), b∼N(0,σ2bI)로 가중치와 바이어스에 모두 적용된다. 가중치와 바이어스 매개변수는 독립적이고 동일 분포 (i.i.d.) 로 간주되므로 i≠j 일 때, 입력 xi 와 xj 는 독립적이며, 함수 g(x) 는 i.i.d. 항의 합이다.
따라서 서로 다른 입력 x 에서 파생된 g(x) 의 유한 집합은 결합 다변량 정규분포라고 추론할 수 있으며, 이를 가우시안 프로세스의 정의와 일치한다.
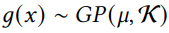
where
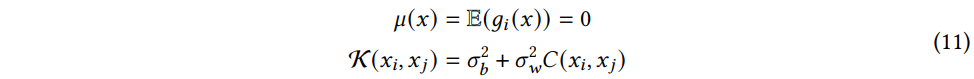
where C(xi,xj) is the covariance between the input x_i and x_j.
(Neural Network Gaussian Process Imputator) 데이터 대치를 위한 NNGPI의 핵심은 가우시안 프로세스에 의한 딥러닝 모델 학습이다.
일반적인 신경망의 경우, 계층의 수나 차원과 같은 하이퍼파라미터에 크게 의존하다. 또한, 모델의 추론은 학습된 결정론적인 가중치를 기반으로 하는데, 이는 과적합 문제를 유발할 수 있다. 반면, 일반적인 GP 접근 방식은 학습된 사전 분포에서 모델의 가중치를 학습된 사전 분포에서 모델의 가중치를 샘플링하여 이러한 문제를 완화시킬 수 있다. 사전 분포에 사용되는 하이퍼파라미터는 일반적인 신경망에 비해 매우 적다. 또한, 단일 결정론적인 가중치에 의존하지 않고 매개 변수의 모든 잠재적 사후 분포에 가중치를 부여하여 과적합 문제를 완화할 수 있다. 하지만, 일반 GP에 사용되는 기본 함수의 본질적인 제한적 근사화 능력으로 인해 주어진 데이터셋의 복잡한 패턴을 정확하게 모델링하는 능력이 제한된다.
신경망의 근사화 능력을 더 잘 활용하기 위해 Neural Network Gaussian Process (NNGP)가 제안되었다. NNGP는 신경망과 GP의 강점을 결합한 베이지안 딥러닝 모델의 특별한 범주이다.
(Neural Network → Gaussian Process) 신경망 관점에서 볼 때 NNGP의 hidden layer는 뉴런의 수가 무한하다는 특정이 있다. 이러한 무한한 hidden neuron 들은 GP의 기저함수를 사용하여 구성된다. 딥러닝 모델의 보편적인 표현 학습 기능을 활용함으로써 이 딥러닝 기반 커널은 데이터에 적응할 수 있는 향상된 유연성을 제공한다.
(Gaussian Process → Neural Network) GP관점에서 보면 NNGP는 무한한 수의 기저함수로 구성되어 있어 데이터셋 내의 복잡한 패턴을 포착할 수 있는 훨씬 더 큰 모델 공간을 확보할 수 있다. 특히, NNGP는 ReLU 활성화 함수와 같은 특정 신경망 구조를 위한 분석 커널 함수 (analytical kernel function) 도 있다. 이 분석 커널 함수는 NNGP의 훈련 및 추론 프로세스가 일반 GP와 유사하게 닫힌 형태로 풀릴 수 있음을 의미한다.
Example) L 개의 계층을 가지는 신경망을 고려해보자.
l (0<l<L) 번째 계층에서 네트워크 출력의 i-th 구성요소는 다음과 같다.
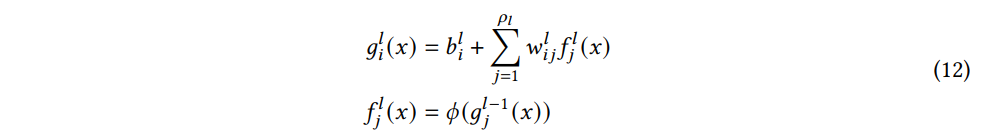
where ρl is the width of layers in layer l (i.e., the number of neurons in layer l) and ϕ(⋅) is the non-linearity function.
(12) 식의 두 번째 식은 gl−1j(x) 라고 가정하면, flj(x) 도 GP 임을 의미한다. gli(x) 가 i.i.d. 항의 합인점을 고려하면, Central Limit Theorem 을 적용할 수 있다. 결과적으로, ρl 이 커질수록 glj(x) 은 정규분포에 가까워진다. 또한, 다차원 CLT를 적용하면 gli(x) 유한한 집합은 결합 다변량 정규분포를 따를 것이다. 이 특성은 정확히 GP의 정의와 일치한다. 입력의 평균이 0이므로 출력은 gli(x)∼GP(0,Kl) 와 같은 GP이다
where Kl is
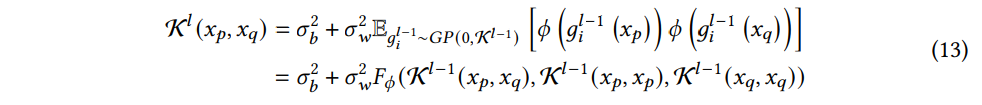
여기서, Fϕ(⋅) 은 Kl−1(xp,xq),Kl−1(xp,xp),Kl−1(xq,xq) 등 이전 계층의 커널 행렬들의 함수이다. 그리고 Fϕ(⋅) 은 비선형함수인 ϕ(⋅) 에만 의존한다. 특정 비선형함수의 경우 점화식 (recurrence relation) 을 계산할 수 있다. 대표적인 비선형 함수인 ReLU의 경우 다음과 같다:
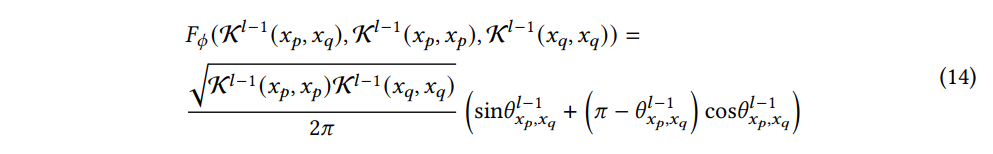
where θlxp,xq is
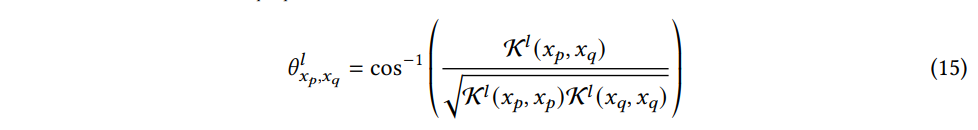
그리고 w0ij∼N(0,σ2w/d0), b0j∼N(0,σ2b) 라고 가정하면, K0는 다음과 같이 초기화한다.
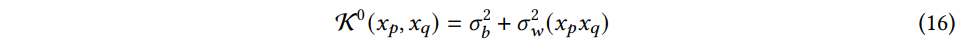
위의 반복 프로세스를 기반으로 일련의 계산을 통해 모델의 최종 출력인 GP에 대한 KL 을 도출할 수 있다. 우리의 목표는 새로운 입력에 대한 예측을 하는 것이다. 테스트 포인트 x∗ 에 해당하는 분포 g(x∗)에 대한 예측은 (9) 식을 적용하여 얻을 수 있다. 사전 분포와 노이즈 분포 모두 정규분포에 속하므로, 출력 P(g(x∗)|g(X)) 또한 다음과 같은 평균 분산을 가지는 정규분포이다:
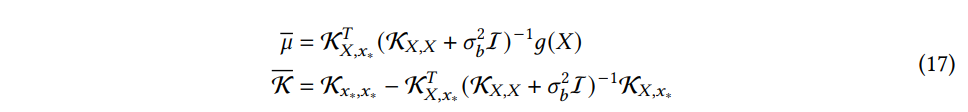
P(g(x∗)|g(X)) 에 대한 예측 분포는 간단한 행렬 계산을 통해 얻을 수 있다. 신경망 모델의 깊이, 비선형 함수의 유형, 가중치 및 바이어스의 분산에 영향을 받는 GP의 사전분포의 선택에 따라 사용되는 공분산 함수의 형태가 결정된다.
(3) Uncertainty-based Calibration
NNGPI를 기반으로 w와 b에 대한 확률 분포는 g(x∗) 에 대한 확률분포를 유도한다. 테스트 데이터 x∗가 주어지면 식 (17) 에 의해 예측된 평균과 분산을 계산할 수 있다. 분산이 작으면 테스트 데이터와 학습 데이터가 유사하다는 것을 나타낸다. 따라서 x∗ 에 대한 예측의 신뢰 구간은 다음과 같이 계산할 수 있다.
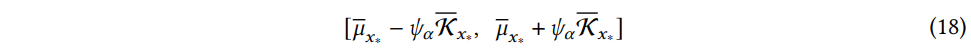
where ˉμx∗ and ˉKx∗ is the predicted target and variance for x_* , respectively. ψα represents the Z-score associated with the confidence level α of N(0,1).
신뢰 구간은 범위에서 실제 값이 속할 확률이 α 임을 나타낸다. 또한, 신뢰 수준 α가 주어지면 위의 신뢰 구간은 분산 ˉKx∗ 과 양의 관계를 가진다. 즉, 테스트 데이터의 분산이 높다는 것은 해당 데이터 포인트가 더 넒은 범위에 속할 가능성이 있다는 것을 의미하며, 이는 불확실성이 높다는 것을 나타낸다.
이전에 연구되었던 바와 같이 GP의 불확실성은 학습된 네트워크 예측 오류와 밀접한 상관관계가 있다. 따라서 데이터셋을 보정하기 위해 불확실성 기반 데이터 보정 접근 방식을 설계한다. 구체적으로, 테스트 데이터 x∗ 가 주어지면 m 번째 반복의 타겟값은 다음과 같이 보정된다.
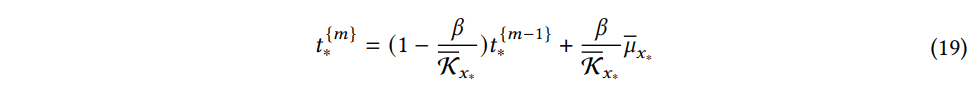
where β∈(0,1) is a coefficient to balance the previous data and the new predicted data.
Learning Objectives
누락된 데이터 대입을 위해 설계된 NNGPI의 학습 목표는 평균 제곱 오차 (MSE) 지표를 사용해 공식화한다. 이는 예측과 실제 레이블 사이의 불일치를 측정하는 것을 목표로 한다. 편차가 더 클수록 큰 패널티를 주므로 이상치에 더 민감하게 반응한다. 또한 신경망 학습을 용이하게 만드는 차별화되고 부드러운 손실 표면 (smooth loss surface)를 제공한다.
Example) 입력 샘플이 다음과 같은 훈련 데이터 세트 X=x1,x2,⋯,xn 과 각각의 ground-truth 라벨 T=t1,t2,⋯,tn 을 고려해보면, 손실함수는 다음과 같이 써진다.
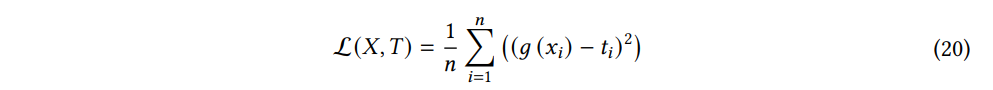
[Algorithim] Forward Propagation of NOMI

테스트 샘플 x∗. 훈련 데이터셋 X,T, 이웃 세트 크기 K, 임계값 τ, 배치 크기 nB 를 입력으로 받는다. 먼저 x∗ 의 결측값이 초기화 되고, 훈련 샘플 배치가 선택된다. NOMI 알고리즘은 예측된 불확실성이 주어진 임계값 τ 보다 작아질 때 까지 여러 번의 반복을 실행한다.
각 반복에서 (1) 검색 모듈, (2) NNGPI, (3) 불확실성 기반 보정을 순차적으로 수행한다.
(1) 검색 모듈에서는 훈련 샘플과 테스트 샘플 모두 증강하고, 각 레이어에서 데이터 샘플의 쌍별 상관관계를 계산한다.
(2) NNGPI는 예측된 대치 값과 불확실성을 모두 출력해준다.
(3) 그 다음으로 데이터를 보정한다. 학습된 불확실성이 주어진 임계값보다 낮으면 알고리즘이 종료되고, 마지막으로 대치가 반환된다.
Multi-Round imputation 의 목적은 1) 좋은 이웃찾기: 보정 후 데이터셋이 원래 분포에 더 가까워져서 원본 데이터셋에 비해 이웃 정보가 개선된다. 2) 불확실성 감소: 반복 횟수가 증가함에 따라 불확실성이 점차 감소하므로 향상된 대치로 이어진다.

Theoretical Analysis
NOMI as an EM algorithm
(EM algorithm) EM 알고리즘은 잠재 변수가 있는 확률 모델에서 매개변수를 추정하는 데 사용되는 반복적 최적화 방법이다. 핵심 아이디어는 Expectation (E) 와 Maximization (M) 단계를 번갈아 가며 수행하며 매개변수를 점진적으로 최적화한다는 것이다. 관측된 데이터셋 xini=1, 잠재 변수 z∈Z, 모델 파라미터 θ 가 주어졌을 때, 관측된 데이터셋과 잠재변수에 대한 결합 분포, 즉 가능도 함수 P(xi,z|θ) 를 최대화하는 것을 목표로 한다. 가능도 함수의 최댓값을 직접 계산하는 것은 많은 비용이 들기 때문에 EM 알고리즘은 가능도 함수의 하한을 최적화 하는 것을 목표로 한다. 이 알고리즘은 다음과 같은 로그 형태를 사용하며 젠센 부등식에 의해 하한이 정해질 수 있다:
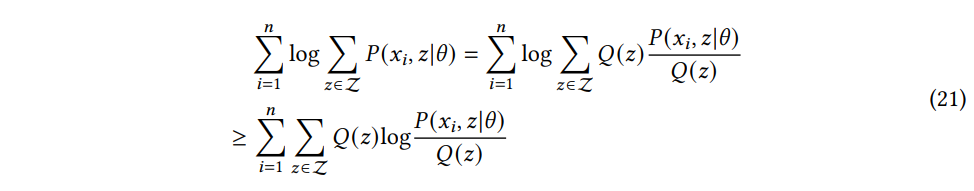
where Q(z) is the weight for the corresponding latent variable.
가능도 함수를 최대화 하는 것이 목표이기 때문에, 가능도 함수의 하한을 최적화해야 한다. 즉, $Q(z) \log \cfrac{p(x_i,z | \theta)}{Q(z)} 를 최적화해야 한다.
E-step) m-th 반복에서 관측된 데이터셋 xini=1, 잠재변수 z∈Z의 사후분포, 이전 반복의 모델 파라미터 θm−1 가 주어졌을 때, E-step에서는 가능도 함수의 기댓값을 계산한다.
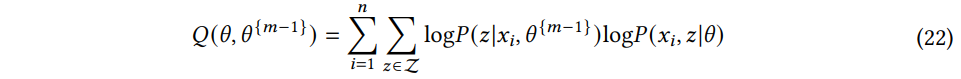
M-step) 모델 파라미터 θm 을 얻기 위해 가능도 함수의 기댓값 Q(θ,θm−1) 를 최대화한다.
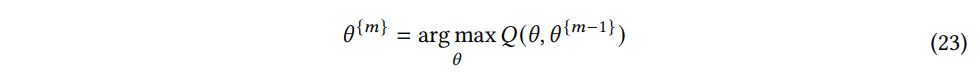
Gradient descent 방법은 일반적으로 기울기가 0과 같아 최대 또는 최솟값에 도달했음을 나타내는 지점을 식별하여 확률 함수를 최대화 하는데 사용된다. 기계 학습에서 큰 데이터셋을 처리할 때, 전체 기울기를 계산하면 계산 비용이 많이 들 수 있다. 따라서 이에 대한 대안으로 확률적 EM 알고리즘이 제안되었다. 확률적 EM 알고리즘은 관측치의 일부 배치만 사용하여 Gradient descent 를 계산한다.
결측치 대치의 맥락에서 데이터 행렬에는 일정 비율의 결측값이 포함되어 있지만 실제 데이터 행렬 (ζ: Clean data matrix) 은 함께 사용할 수 없다. 클린 데이터 행렬을 잠재 변수로 취급하고 훈련 데이터셋의 데이터는 타겟과 함께 xi,tini=1 을 관측된 데이터로 사용한다. 그러므로 EM 은 다음과 같은 가능도를 최대화하는 것을 목표로 한다.
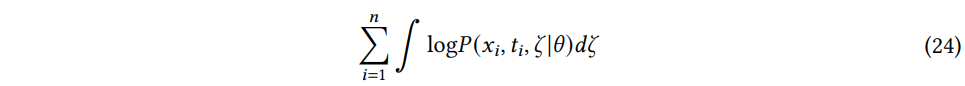
E 단계에서는 NOMI의 프레임워크 내에서 불확실성 기반 데이터 보정단계에 해당한다. m-th 반복의 E단계에서는 확률 함수의 예상값을 계산한다.
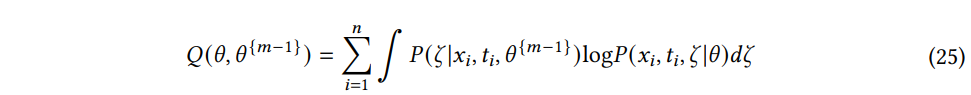
where P(ζ|xi,ti,θm−1) is posterior distribution of the clean data matrix ζ given the training dataset and the learned model parameter.
확률적 EM 알고리즘에서 클린 데이터 행렬 ζ의 사후분포 P(ζ|xi,ti,θm−1) 은 δ-분포를 이용하여 근사화된다. δ-분포는 데이터 보정 단계에서 얻어진 사후 분포의 기댓값 ζm−1에 집중시킨다. 그러므로 E-step은 NOMI 의 프레임워크 내에서 불확실성 기반 데이터 보정 단계에 해당하고 다음과 같이 근사시킬 수 있다:
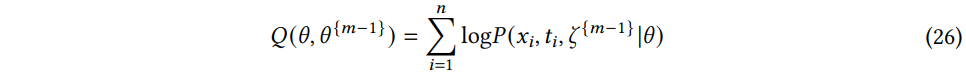
(Step by Step) 직접 유도한거라 실수가 있을 수도 있음 주의!

M 단계는 NOMI의 프레임워크에서 NNGPI 단계에 해당한다. M 단계에서는 식(26) 에 정의된 가능도 함수의 기댓값을 최대화하는 것이 목표이다. 확률적 EM 알고리즘에서 이 함수는 제한된 레이블된 데이터에 대해 확률적 경사하강을 사용하여 최적화된다. 이 맥락에서, θm은 사전 분포와 관련된 모든 매개변수를 나타낸다. 그리고 모델 은 가능도 함수의 기댓값을 최대화하여 최적의 파라미터 θm을 학습한다.
이러한 재구성을 통해 NOMI는 EM 알고리즘의 좋은 특성을 이어받았다. EM 알고리즘은 수렴에 도달할 때 까지 각 반복 과정에서 로그 가능도의 값이 점진적으로 증가하도록 보장하므로 반복할수록 NNGPI의 대치 능력이 증가한다. 여러번의 반복을 통해 NNGPI와 불확실성 기반 보정 모두 가장 최근의 신뢰할 수 있는 정보를 합쳐 높은 품질의 대치를 이끌어낸다. 또한 불확실성 기반 보정을 통해 보다 신뢰할 수 있는 mini-batch gradient 를 얻을 수 있으므로 완전히 관찰된 깨끗한 데이터셋에서 도출된 기울기와 더 잘 정렬할 수 있다. 이러한 정렬을 통해 확률적 EM 알고리즘을 바이어스 없이 갱신할 수 있으므로 NNGPI의 전반적인 효율성이 향상되고 불확실성 기반 보정 단계를 지원할 수 있다.
Conclusions
대치 성능을 향상시키기 위해 검색 모듈, NNGPI, 불확실성 기반 보정 모듈을 통합한 새로운 모델인 NOMI 를 제안했다. 이러한 모듈은 반복적으로 실행된다. NNGPI는 심층 신경망의 예측 능력과 가우시안 프로세스의 불확실성 추정 능력을 모두 결합하여 과적합 문제를 완화하면서 누락된 데이터와 불확실성을 모두 예측한다. 또한 학습된 불확실성을 활용하는 불확실성 기반 보정 모듈을 설계하여 검색 모듈이 보다 안정적이고 정확한 로컬 정보를 얻을 수 있도록 지원한다.
'Statistics' 카테고리의 다른 글
| CLAIM Your Data: Enhancing Imputation Accuarcy with Contextual Large Language Models (1) | 2024.06.12 |
|---|---|
| 등회귀 (Isotonic Regression) (0) | 2023.12.15 |
| [Statistics] MAP estimation 이란? (1) | 2023.10.02 |


