Intro
X와 Y의 관계가 선형이 아닌, 비선형(non-linear) 문제는 어떻게 해결해야할까?
비선형 회귀의 종류는 다음과 같다.
| 등회귀(Isotonic Regression) | 비선형이고, x가 커질 때 y도 같이 커지는(monotonous increase) 경우 |
| 다항회귀(Polynomial Regression) | 비선형이고, non-monotonous일 경우 |
| 국소 회귀(Local Regression) | 비선형이지만 국소 지역에 한해서 선형 관계를 띈다고 가정할 경우 |
이번 포스팅에서는 등회귀(Isotonic regression)에 대해 알아보자.
등회귀와 PAVA
등회귀의 isotonic의 어원을 살펴보자. “iso” 는 ‘동일하다’ 는 그리스어에서 파생되었고, “tonos” 는 ‘잡아늘이다’ 라는 뜻이 있다. 즉, 데이터 포인트의 위치가 동일해지도록 ‘잡아끌어올리는’ 회귀식인데 그림으로 먼저 살펴보자.
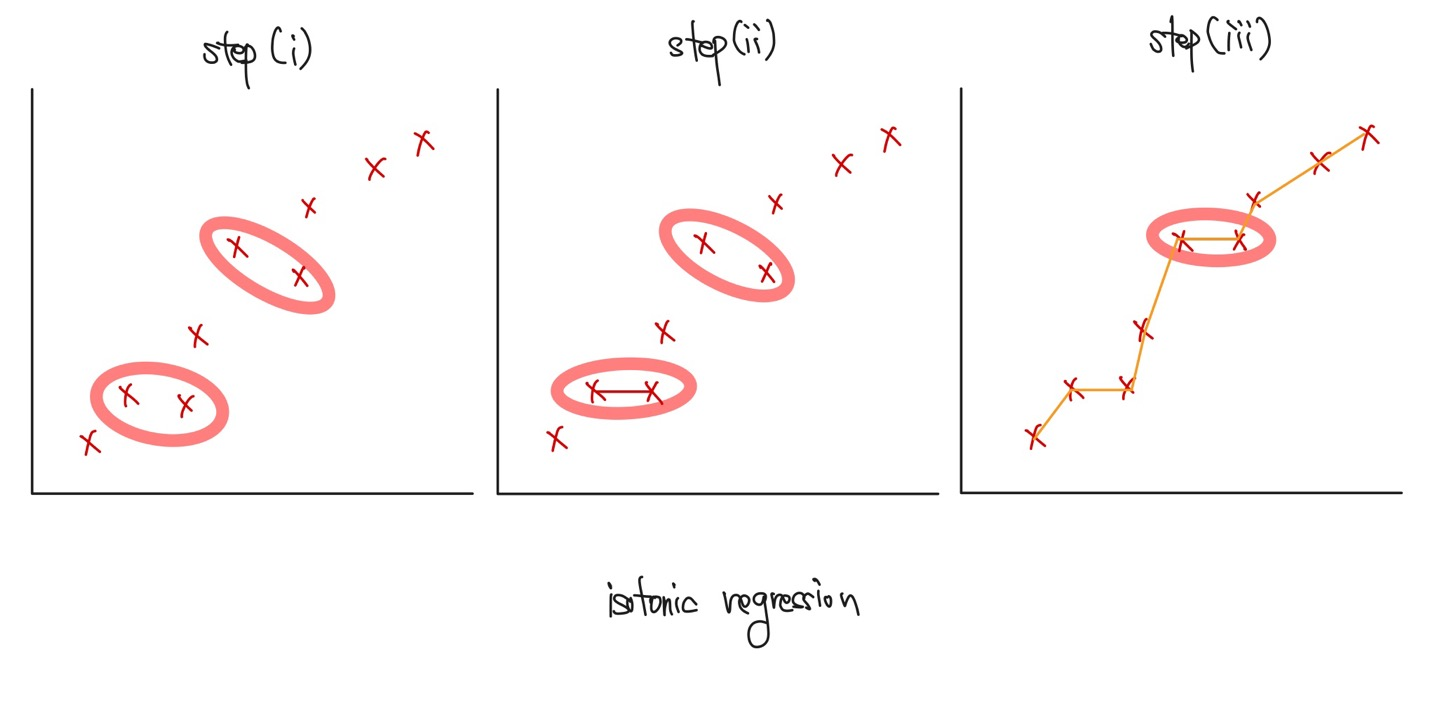
일단 등회귀를 쓰기 위해서는 타겟 함수가 단조 증가 함수(monotonous function)이어야 한다. 단조 함수는 x1 < x2 일 때, f(x1) ≤ f(x2) 인 함수를 말한다. 그런데 위의 도표 step(i)을 보면 f(x3)은 f(x2)보다 그 값이 작다. 단조 함수의 규칙에 어긋나는 또 다른 지점도 빨간 원으로 표기해두었다.
등회귀는 이런 어긋나는 지점을 해결하는데 이 글에서는 가장 간단한 알고리즘인 PAVA(Pool Adjacent Violators Algorithm)를 설명한다.
- 첫 단계에서는 규칙에 어긋나는 데이터를 찾는다. 예를 들어, f(xi)가 f(xi+1)보다 큰 지점을 찾는 것이다.
- 두 번째 단계에서는 f'(xi)값을 f'(xi+1)값에 대입하여 SSE(Sum of Squared Errors, 오차제곱합)을 최소화 한다. 그림으로 이해하자면 f(x3)값을 f(x2) 위치로 끌어 올리는 과정을 말한다.
- 이런 식으로 x값이 커짐에 따라 단조 증가 함수의 규칙에 어긋나는 데이터 지점을 모두 끌어 올리고 각 지점을 부분 선형 함수(piecewise linear function)로 연결하면 끝이다.
등회귀는 언제 사용되나?
등회귀는 통계적 추론에 사용된다. 예를 들어, x의 순서에 따라 y값이 증가할 것으로 예상되는 데이터 셋의 경우, 등회귀식을 적용할 수 있다. 분류(classification) 문제에서는 모델의 예측값을 보정(calibration)할 때도 사용된다.
'Statistics' 카테고리의 다른 글
| CLAIM Your Data: Enhancing Imputation Accuarcy with Contextual Large Language Models (1) | 2024.06.12 |
|---|---|
| Missing Data Imputation with Uncertainty-Driven Network (2) | 2024.06.10 |
| [Statistics] MAP estimation 이란? (1) | 2023.10.02 |


