[NLP] Attention is All You Need

Submit date : 12 Jun 2017 
Archive Link
https://arxiv.org/abs/1706.03762

Attention Is All You Need

 
 Attention is All You Need, Transformer 논문 리뷰를 시작해본다.
사실 논문 리뷰가 아니라 Transformer 모델을 하나하나 뜯어서 공부한 내용을 담아봤다. 고로 다소 길어짐
 
*참고로, 이번 리뷰에서는 Jay Alammar의 Transformer 설명에 나오는 그림들을 사용했다.
http://jalammar.github.io/illustrated-transformer/

The Illustrated Transformer

 
  Attention is All You Need 는 딥러닝을 활용한 Natural Language Processing(NLP)에서 가장 큰 변화를 가져온 논문이다. 이 논문 이후로 더 이상 RNN, CNN 등을 활용한 자연어 처리 연구는 거의 이루어지지 않는 것 같다.  딥러닝을 활용하여 NLP를 한다면, 앞으로는 해당 논문에서 제시한 Transformer 구조나, 이를 변형한 BERT등의 구조를 사용함이 바람직해보인다.
 

💡Abstract

 현재 대부분의 Sequence Model은 CNN이나 RNN을 Encoder, Decoder로써 활용하고 있다. 그 중 가장 좋은 성능을 보이는 모델은 Attention mechanism을 활용한 Encoder, Decoder모델이다. 본 논문은 CNN과 RNN을 없애고 Attention mechanism에만 기반을 둔 단순한 Network인 Transformer를 제안한다.
 그 결과 P100 GPU 8대로 SOTA 성능을 달성한 빠르고 좋은 모델임을 증명해냈다. 이유는 바로 효율적인 병렬처리 때문인데, 이에 대한 것은 글을 써내려가면서 상술할 예정이다.
 

✏️Background

  LSTM과 GRU 와 같은 Recurrent Neural Network(RNN)는 Sequence Modeling 분야 에서 대부분의 State-of-the-Art(SOTA)성능을 제공하고 있다. 이 모델들은 Input sequence 를 순차적으로 입력받는데, 입력받는 시점 t 에서 해당 Input과 이전 hidden state ht−1 을 기반으로 현재 hidden state ht 를 생성한다. 이렇게 모든 처리를 순차적으로 해야하는 특징 때문에, 여러 작업을 동시에 수행하지 못했고, 당연히 병렬처리의 효율도 떨어지게 되었다. 이러한 문제들을 해결하기 위해 최근에는 factorization trick이나 conditional computation 등의 방법들이 제안되었지만, 순차적으로 데이터를 처리한다는 큰 틀은 벗어나지 못하고 있다. 순차적으로 데이터를 처리할 때 발생하는 이러한 문제들을 해결하기 위해서 ByteNet, ConvS2S 등과 같이 Convolutional Neural Network(CNN)을 사용하는 경우들도 있다. 하지만 CNN을 사용하는 경우, 입력의 길이가 길어질수록 입력의 원소와 출력의 원소 사이의 의존성을 학습하기 위한 거리가 매우 길어진다는 문제가 있다.

Attention mechanism은 Sequence Modeling을 할 때 입력과 출력의 원소들 사이의 거리와 무관하게 의존성(dependency)를 학습할 수 있다. 대부분의 경우 Attention은 기존의 RNN과 함께 사용되어 왔다. 
 
 이번 논문에서는 Transformer를 제안한다. Recurrence를 제거함으로서 위에서 언급한 문제들을 해결하고, 오직 Attention mechanism 만을 이용해서 입력과 출력 사이의 global dependency 를 학습하게 된다. Recurrence가 없어졌으니 당연히 더 손쉽게 병렬처리가 가능해진다. 또한, CNN을 사용했을 때 문제였던 원소들 사이의 거리가 매우 멀어지는 문제도 상수개의 연산으로 고정시킬 수 있는 매우 큰 장점이 있다. Transformer의 가장 큰 특징 중 하나는 Self-Attention을 수행한다는 것이다. Self-Attention은 동일한 sequence(입력, 출력 등) 내의 원소들 사이에서 Attention을 수행하는 것이다. 참고로, Self-Attention은 Transformer에서 처음 사용된 것은 아니고, reading comprehension, abstractive summarization 등의 분야에서 많이 사용되고 있는 기법 중 하나이다.
 

🛠 Model Architecture

 공부한 내용을 다 써놓다보니 다소 내용이 길어짐 주의!
 
 가장 뛰어난 Sequence Model은 Encoder-Decoder구조를 활용한다. Encoder가 symbol representation x1, .., xn을 가지고 있는 Input sequence를 연속적인 representation  z1, .. ,zn으로 바꿔준다. 그리고 그 z를 가지고 Decoder가 순차적으로 symbol을 가진 output sequence y1,.. ,ym 을 만들어낸다. 이때 symbol을 만드는 과정은 Auto-Regressive(AR)인데 이는 각 yi를 만들어내는 단계에서는 이전의 만들어진 symbol도 Input으로 사용한다는 의미이다.
 
 Transformer는 다음의 구조를 가지는데, Self-Attention의 stack version과 Encoder와 Decoder 모두 Fully Connected Layer (FC Layer)를 가진 형태이다.

 전체적인 Transformer 구조는 너무 유명한 그림이라 한번 첨부해봤다. 이제 하나하나 뜯어보며 공부해보자. 

 먼저 모델의 자세한 부분을 무시하고, 이를 하나의 black box라고 생각해보자. Machine Translation의 경우를 생각해본다면, 다음과 같은 그림처럼 모델은 어떤 한 언어로 된 하나의 문장을 입력으로 받아 다른 언어로 된 번역을 출력으로 내놓을 것이다.

 이제 black box를 구성하는 Encoder들, Decoder들, 그리고 그 사이를 이어주는 Connection들을 들여다볼 것이다.

 위의 왼쪽 그림과 같이 Encoders 부분은 오른쪽 그림과 같이 여러 개의 Encoder들을 쌓아 올려 만든 것이다. 왼쪽 그림에서 Encoders라고 표현한 이유이다. 마찬가지로 Decoders 부분은 Encoder 부분과 동일한 개수만큼의 Decoder 을 쌓아 만들었다. 각 Encoder, Decoder들끼리는 모두 같은 구조를 가지고 있다. 그러나 같은 weight을 공유하진 않는다. 

*논문에서는 6개를 쌓았지만, 이는 하이퍼파라미터로 각자의 세팅에 맞게 얼마든지 변경하여 실험할 수 있다.

 이제 하나의 Encoder를 들여다보면 아래의 그림과 같이 두 개의 sub-layer으로 구성되어 있다.

 Encoder에 들어온 입력은 일단 먼저 Self-Attention 층을 지나가게 된다. 이 층는 Encoder가 하나의 특정한 단어를 Encoding 하기 위해서 입력 내의 모든 다른 단어들과의 관계를 살펴본다. 개략적인 설명을 위해 Self-Attention 층에 대해서는 후의 자세히 서술해보겠다.

 Input이 Self-Attention 층을 통과하여 나온 Output은 다시 Feed Foward Neural Network(FFNN)으로 들어가게 된다. 똑같은 FFNN이 각 위치의 단어마다 독립적으로 적용되어 Output을 만들게 된다.

 마찬가지로 Decoder도 두개의 층을 모두를 가지고 있다. 그러나 그 두 층 사이에 Encoder-Decoder Attention 이 포함되어 있다. 이는 Decoder가 Input Sequence중에서 각 시점t 에서 가장 관련 있는 부분에 집중할 수 있도록 해준다.

🛠 Model Architecture - 더 자세히 들여다보기

- Encoder 

1. Embedding

 이제 입력으로 들어와서 출력이 될 때까지 이 부분들 사이를 지나가며 변환될 벡터/텐서들을 기준으로 모델을 살펴보도록 하자.

 현대에 들어 대부분 NLP 관련 모델에서 그러듯, 먼저 입력 단어들을 embedding 알고리즘를 이용해 벡터로 바꾸는 것부터 해야한다.

 

 각 단어들은 크기 512의 벡터 하나로 embed 하면 이 변환된 벡터들을 위와 같은 간단한 박스로 나타내볼 수 있다.

 이 embedding은 가장 밑단의 Encoder에서만 일어난다. 이렇게 되면 이제 우리는 이렇게 뭉뚱그려 표현할 수 있게 된다. 모든 Encoder 들은 크기 512의 벡터의 리스트를 입력으로 받게된다. 이 벡터는 가장 밑단의 Encoder의 경우에는 word embedding이 될 것이고, 나머지 Encoder들에서는 바로 전의 Encoder의 출력일 것이다.

 이 벡터 리스트의 사이즈는 hyperparameter으로 우리가 마음대로 정할 수 있다. 예를 들어, 가장 간 학습 데이터 셋에서 가장 긴 문장의 단어 개수, 상위 95%에 해당하는 Token의 개수 등을 생각해볼 수 있다.

 

2. Positional Encoding 

 우리가 이때까지 설명해온 Transformer 모델에서 한가지 부족한 부분은 에서 단어들의 순서에 대해서 고려하고 있지 않다는 점이다. 

 이를 고려하기 위해서, Transformer 모델은 각각의 Input embedding에 동일한 차원을 갖는 “Positional Encoding”이라고 불리는 하나의 벡터를 추가한다. 이 벡터들은 모델이 학습하는 특정한 패턴을 따르는데, 이러한 패턴은 모델이 각 단어의 위치와 Sequence 내의 다른 단어 간의 위치 차이에 대한 정보를 알 수 있게 해준다. 이 벡터들을 추가하기로 한 배경에는 이 값들을 단어들의 embedding에 추가하는 것이 Query/Key/Value 벡터들로 나중에 투영되었을 때 단어들 간의 거리를 늘릴 수 있다는 점이 있다.

 결국 Positional Encoding 벡터를 도입하는 궁극적인 이유는 각 단어의 위치와 Sequence 내의 다른 단어 간의 위치 차이에 대한 정보를 알 수 있게 해줌으로써 모델에게 단어의 순서에 대한 정보를 주기 위함이다.

 

 다음은 대표적인 Positional Encoding 방법이다.

 pos는 Input sequence에서 임베딩 벡터의 위치(position)을, i는 임베딩 벡터의 차원 (Transformer 같은 경우 512)을 의미한다. 각 i가 짝수일 때는 sin함수, 홀수일 때는 cos함수를 사용하여 Input sequence에 특정 순서를 부여한다.
 
 예를 들어 "My friend came over to my house" 라는 문장이 있을 때, my라는 단어를 두 번 사용한다. 이때 각 my의 위치는 다르다. 즉, 위의 식을 기준으로 pos값이 다르다. 그러므로 Positional Encoding을 진행할 때 pos에 따라 임베딩 벡터의 값은 다르게 들어갈 것이며, 그로 인해 순서 또한 부여될 것이다. 실제로 20개의 단어로 이루어진 문장에 대한 Positional Encoding을 진행한 결과를 아래 이미지를 통해 확인해볼 수 있다.

 중간을 기점으로 왼쪽은 sin함수에 대하여 생성된 Positional Encoding이며, 오른쪽은 cos함수로 인해 생성된 것이다. 이 두 값들은 연결되어 하나의 Positional Encoding vector로 통합된다. 

 구체적인 예시를 통해 알아보자. 만약 embedding의 사이즈가 4 (i=4) 라고 가정한다면, 실제로 각 위치에 따른 Positional Encoding은 아래와 같다.

 또 다른 예시를 들어보면,  표현을 이해하기 위해 n=100, d=4인 “I am a robots" 이라는 문구가 있다.  다음 표는 이 문구에 대한 Positional Encoding matrix를 보여준다. 실제로 Positional Encoding matrix은 n=100이고 d=4인 4글자 모든 구문에 대해 동일하다.

Positional Encoding matrix

 
좋은 Positional Encoding vector가 되기 위해서는 두가지 특성을 지니어야한다.
 
1) Encoding vector의 norm이 모든 위치에서 같아야한다.
 
  다음은 100개의 Token의 512차원 Positional Encoding vector의 L2-norm을 나타낸 것이다.

 평균은 256.12, 표준편차는 1.35 인것으로 보아 평균에 비해 표준편차가 매우 작으므로 첫번째 조건을 만족함을 알 수 있다.
 
2) 두 Encoding vector의 위치가 멀수록 그 거리가 멀어져야 한다.
 
  다음은 10개의 Token의 10차원 Postional Encoding vector 사이의 거리를 나타낸 matrix이다.

  다음은 100개의 Token의 512차원 Postional Encoding vector 사이의 거리를 나타낸 matrix이다.

 대각원소들의 값이 작고 비대각원소들의 원소가 큰 것으로 보아 두번째 조건도 만족시킴을 알 수 있다.
 
이후 각 단어에 해당하는 벡터들은 Encoder 내의 두 개의 sub-layer으로 들어가게 된다.

 여기서 우리는 각 위치에 있는 각 단어가 고유의 path를 통해 Encoder에서 흘러간다는 Transformer 모델의 주요 성질을 볼 수 있다. Self-Attention 층에서 이 위치에 따른 path들 사이에 다 dependency가 있다. 반면 Feed Forward 층은 이런 dependency가 없기 때문에 Feed Forward layer 내의 이 다양한 path 들은 병렬처리가 가능하다.

 이제 이 예시를 실제 문장을 통해 Encoder의 각 sub-layer에서 무슨 일이 일어나는지를 자세히 보도록 하자.

 

3. Self-Attention

 

 "The animal didn't cross the street beacause it was too tired."

 

위 문장에서 “it” 이 가리키는 것은 무엇일까?

 

“it”은 street을 지칭할까 아니면 animal을 지칭할까?

 

 사람에게는 이것이 너무나도 간단한 질문이지만 신경망 모델에게는 그렇게 간단하지만은 않은 문제이다. 모델이 “it”이라는 단어를 처리할 때, 모델은 Self-Attention 을 이용하여 “it”과 “animal”을 연결할 수 있게된다. 모델이 입력 문장 내의 각 단어를 처리해 나감에 따라, Self-Attention은 입력 문장 내의 다른 위치에 있는 단어들을 보고 거기서 힌트를 받아 현재 타겟 위치의 단어를 더 잘 Encoding 할 수 있게된다.

 즉, Self-Attention의 목표는 동일한 Input sequence에 현재 처리중인 단어의 입장에서 다른 단어를 살펴보는 것이다. 이를 통해  Transformer에서 현재 처리 중인 단어에 다른 연관 있는 단어들의 맥락을 넣어주는 mechanism이다.

 

- Details

 

 step1.

 Self-Attention 계산의 가장 첫 단계는 Encoder에 입력된 각 단어의 embedding vector들로부터 각 3개의 벡터를 만들어내는 일이다. 입력된 각 단어의 embedding vector에 대해서 세 개의 학습 가능한 행렬들(WQ, WK, WV)을 각각 곱함으로써 각 단어에 대한 Query 벡터, Key 벡터, 그리고 Value 벡터를 생성한다.

 

 

 x1를 weight 행렬인 WQ로 곱하는 것은 현재 단어와 연관된 Query 벡터인 q1를 생성한다. 같은 방법으로 각 단어에 대한 Query, Key, Value 벡터를 만들 수 있다.

 그래서 Query, Key, Value 벡터가 의미하는 것이 무엇일까?

 

 

 

 

 

step2.

 Self-Attention 계산의 두 번째 스텝은 점수를 계산하는 것이다. 아래의 첫 번째 단어인 “Thinking”에 대해 Self-Attention을 구해보자. 먼저 이 단어와 입력 문장 속의 다른 모든 단어들에 대해서 각각 점수를 계산해야한다. 이 점수는 현재 위치의 이 단어를 Encoding 할 때 다른 단어들에 대해서 얼마나 집중을 해야 할지를 결정한다. 

 점수는 현재 단어의 Query vector와 점수를 매기려 하는 다른 위치에 있는 단어의 Key vector의 내적으로 계산된다. 다시 말해, Thinking에 대해서 Self-Attention을 계산한다 했을 때, 첫 번째 점수는 q1과 k1의 내적일 것이다. 그리고 동일하게 두 번째 점수는 q1과 k2의 내적으로 구할 수 있다.

step3.

세 번째단계는 이 점수들을 Key vector의 사이즈의 제곱근 √dk (논문에서는 √64 = 8) 로 나눈다. 이 나눗셈을 통해 우리는 더 안정적인 Gradient를 가지게된다. 그리고 난 다음 이 값을 Softmax 계산을 통과시켜 모든 점수들을 확률로 만들고 그 합을 1으로 만들어준다.

 

step3

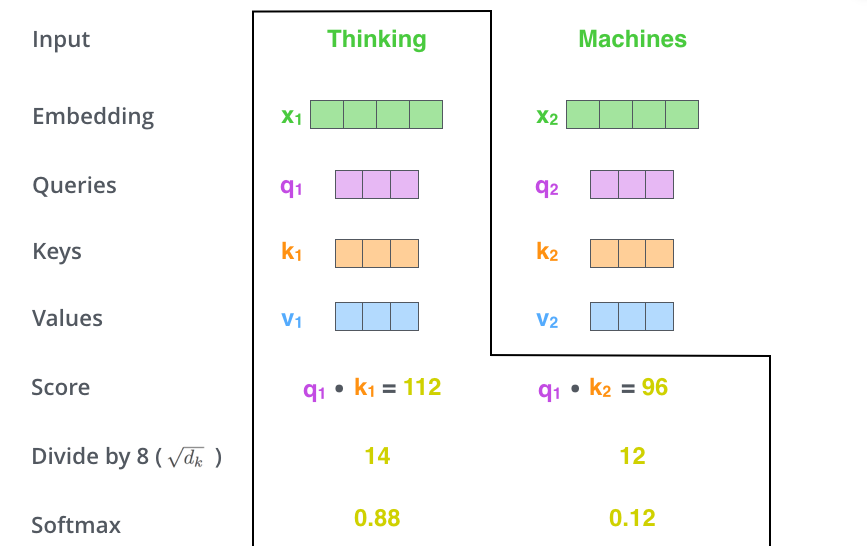
 이 Softmax 점수는 현재 위치의 단어의 Encoding에 있어서 지금 보고 있는 Token에 얼마나 영향을 미치는지 나타낸다. 당연하게 현재 위치의 단어가 가장 높은 점수를 가지며 가장 많은 부분을 차지하게 되겠지만, 가끔은 현재 단어에 관련이 있는 다른 단어에 대한 정보가 들어가는 것이 도움이 된다.

step4.

 이제 입력의 각 단어들의 Value vector에 이 점수를 곱하는 것이다. 이것을 하는 이유는 집중을 하고 싶은 관련이 있는 단어들은 그래도 남겨두고, 관련이 없는 단어들은 작은 점수를 곱해 없애버리기 위함이다.

 

step5.

 마지막 단계는 이 점수로 곱해진 weighted value 벡터들을 다 합해 버리는 것이다. 이 단계의 출력이 바로 현재 위치에 대한 Self-Attention layer의 출력이 된다.

 

 

step4, step5

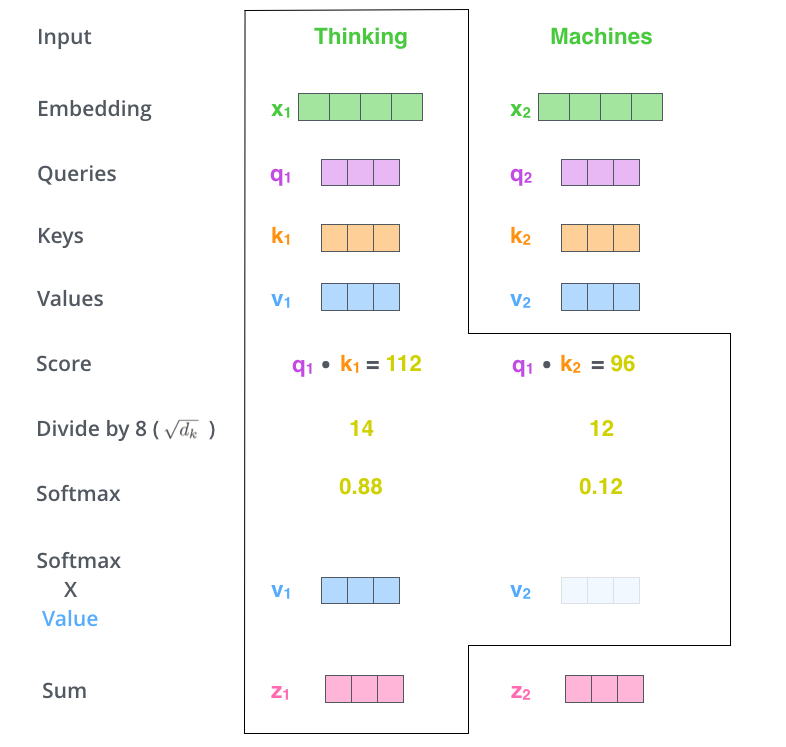
이 과정들이 바로 Self-Attention의 계산 과정이다. 우리는 이 결과로 나온 벡터를 FFNN으로 보내게 된다.

 그러나 실제 구현에서는 빠른 속도를 위해 이 모든 과정들이 벡터가 아닌 행렬의 형태로 진행되므로 이제 이 행렬 레벨의 계산을 살펴보도록 하자.

 

*Self-Attention의 행렬 계산

 가장 첫 단계는 입력 문장에 대해서 Query, Key, Value 행렬들을 계산하는 것이다. 이를 위해 입력 embedding vector들을 하나의 행렬 X로 쌓아 올리고, 그것을 우리가 학습할 weight 행렬들인 WQ, WK, WV 로 곱한다.

 

 행렬 X의 각 행은 입력 문장의 각 단어에 해당한다. 여기서 다시 한번 embedding 벡터들 (크기 512, 그림에서는 4)과 Query, Key, Value 벡터들 (크기 64, 그림에서는 3) 간의 크기 차이를 볼 수 있다.

 마지막으로, 우리는 현재 행렬을 이용하고 있으므로 앞서 설명했던 Self-Attention 계산 단계를 하나의 식으로 압축할 수 있다. 

self-attention 계산 과정

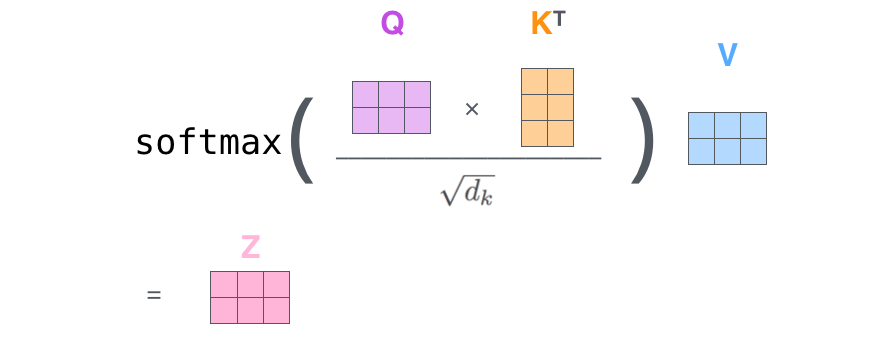
4. Multi-headed Attention

 본 논문은 이 Self-Attention layer에다 “Multi-headed” Attention이라는 메커니즘을 더해 더욱 개선한다. 이것은 두 가지 방법으로 성능을 향상시킨다.

1. 모델이 다른 위치에 집중하는 능력을 확장

   

 위의 예시에서는 z1 이 모든 다른 단어들의 Encoding 을 조금씩 포함했지만, 실제로는 이것은 실제 자기 자신에게만 높은 점수를 줘 자신만을 포함해도 됐을 것이다. 처음에 예시로 들었던  “The animal didn't cross the street beacause it was too tired.” 문장을 번역할 때 “it”이 무엇을 가리키는지에 대해 알아낼 때 유용하다.

 

2.  Attention layer 가 여러 개의 “representation 공간”을 가지게 해준다.

 

 Multi-headed Attention을 이용함으로써 우리는 여러 개의 Query, Key, Value weight 행렬들을 가지게 된다. (논문에서 제안된 구조는 8개의 Attention heads를 가지므로 각 Encoder/Decoder마다 이런 8개의 세트를 가지게 되는 것이다). 이 각각의 Query, Key, Value set는 랜덤으로 초기화되어 학습되고,  각각의 세트는 입력 벡터들에 곱해져 벡터들을 각 목적에 맞게 투영시키게 된다. 이러한 세트가 여러개 있다는 것은 각 벡터들을 각각 다른 representation 공간으로 나타낸 다는 것을 의미한다. 즉, it이 어떤 단어들을 가리키는지에 대한 여러 경우의 수를 염두한다고 볼 수 있다. 

 step1. 

 Input sequence의 각 단어들을 embedding하여 쌓아올려 행렬 X 생성

(첫번째 Encoding 층에서만 해당, 다른 encoding 층에서는 이전 Encoding의 Output을 Input으로 받음)

step2.

WQ, WK, WV를 8개의 head로 나눈다.

 

 각각의 Attention head 별로 들여다보면 다음과 같다.

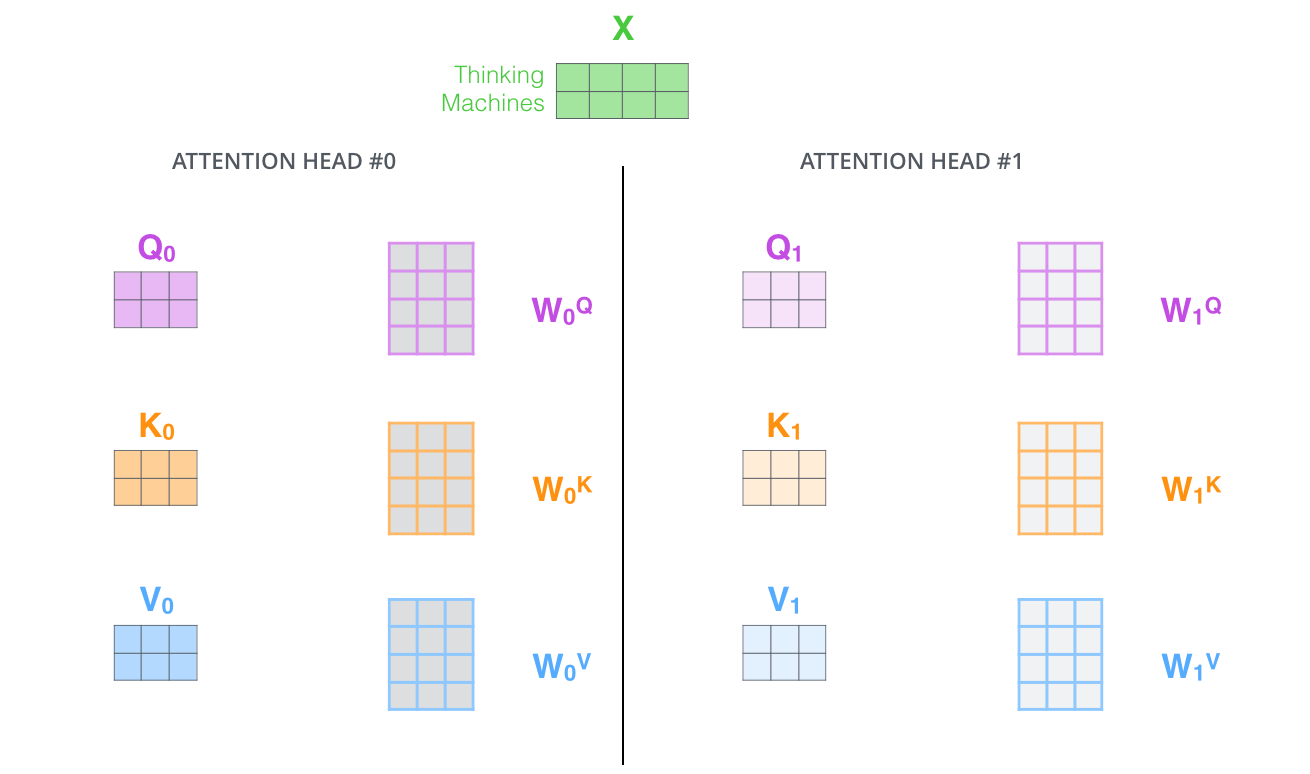
 Multi-headed Attention을 이용하기 위해서 우리는 각 head를 위해서 각각의 다른 Query/Key/Value weight 행렬들을 모델에 가지게 된다. 이전에 설명한 것과 같이 우리는 입력 벡터들의 모음인 행렬 X를 WQ, WK, WV 행렬들로 곱해 각 head에 대한 Q, K, V행렬들을 생성한다.

step3.

 Self-Attention 계산 과정을 8개의 다른 weight 행렬들에 대해 8번 거치게 되면, Attention head만큼의 서로 다른 Z 행렬 8개를 가지게 된다.

step4.

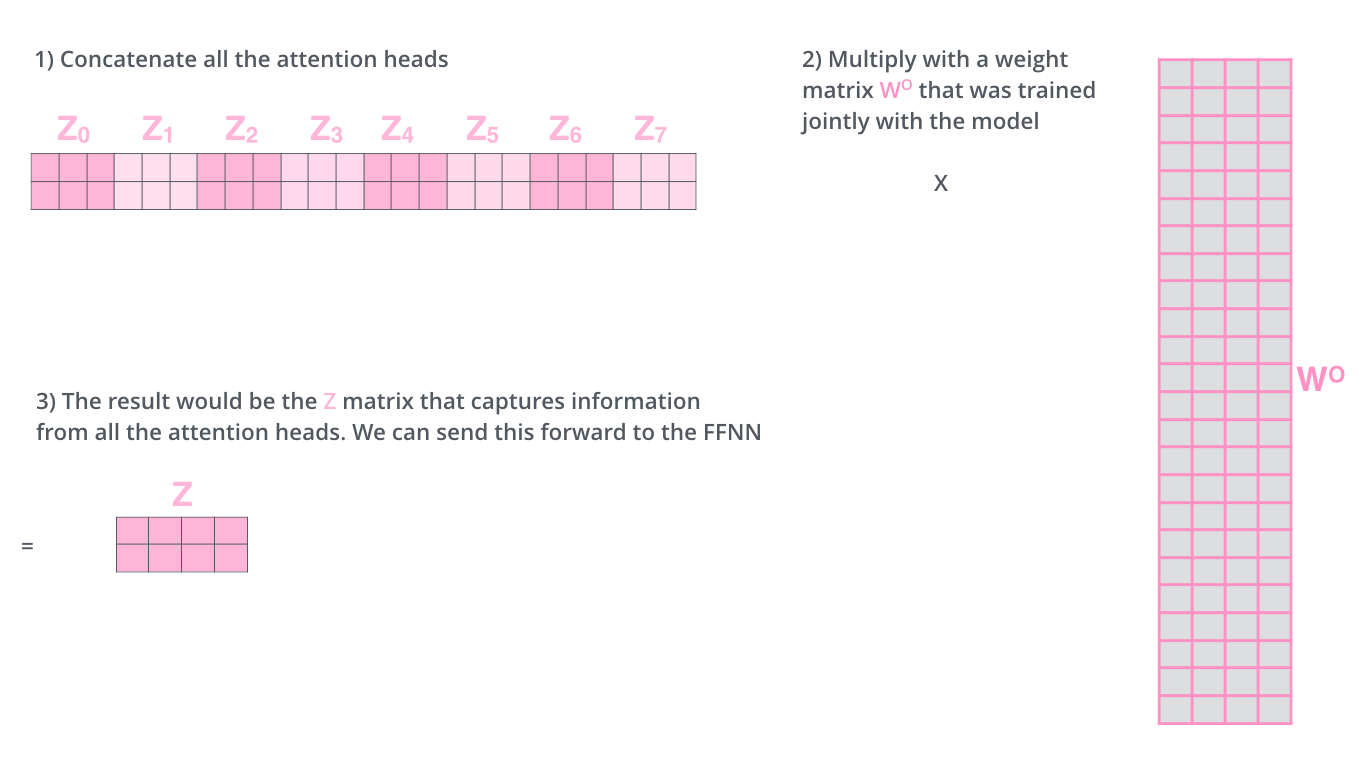
그러나 문제는 이 8개의 행렬을 바로 FFNN으로 보낼 수 없다. FFNN은 한 위치에 대해 오직 한 개의 행렬만을 Input으로 받을 수 있기 때문이다. 그러므로 우리는 이 8개의 행렬을 하나의 행렬로 표현해야한다.

따라서 일단 모두 이어 붙여서(concatenation) 하나의 행렬Z 로 만들어버리고, 그 다음 하나의 또 다른 weight 행렬인 W0을 곱하면 된다.

5. Residual connection & Normalization

 각 Encoder 내의 sub-layer 가 Residual Connection으로 연결되어 있으며, 그 후에는 Layer-normalization 과정을 거친다는 것이다.

 Residual Connection에 대한 설명은 아래 더보기를 참고하세요.

 * Residual Connection? - ResNet에 처음 등장

사람들은 VGG에 따라 깊이가 깊어지면 더 높은 성능을 낼 것이라고 생각하였다. 

 

하지만 점차 레이어가 깊어지면 Vanishing Gradient와 같은 문제가 발생함을 인지하였으며, 따라서 레이어의 깊이가 깊어질수록, Input층에 가까운 hidden layer가 희미해지기에 학습에 도움이 되지 않을수도 있음을 주장하였다. 

 

Plain Netwrok Vs ResNet

Plain Network는 단순히 Convolution 연산을 단순히 쌓는다면, ResNet은 Block단위로 Parameter을 전달하기 전에 이전의 값을 더하는 방식이다. 참고로 ResNet은 딥러닝 이미지 분야에서 바이블로 통하고 있다.

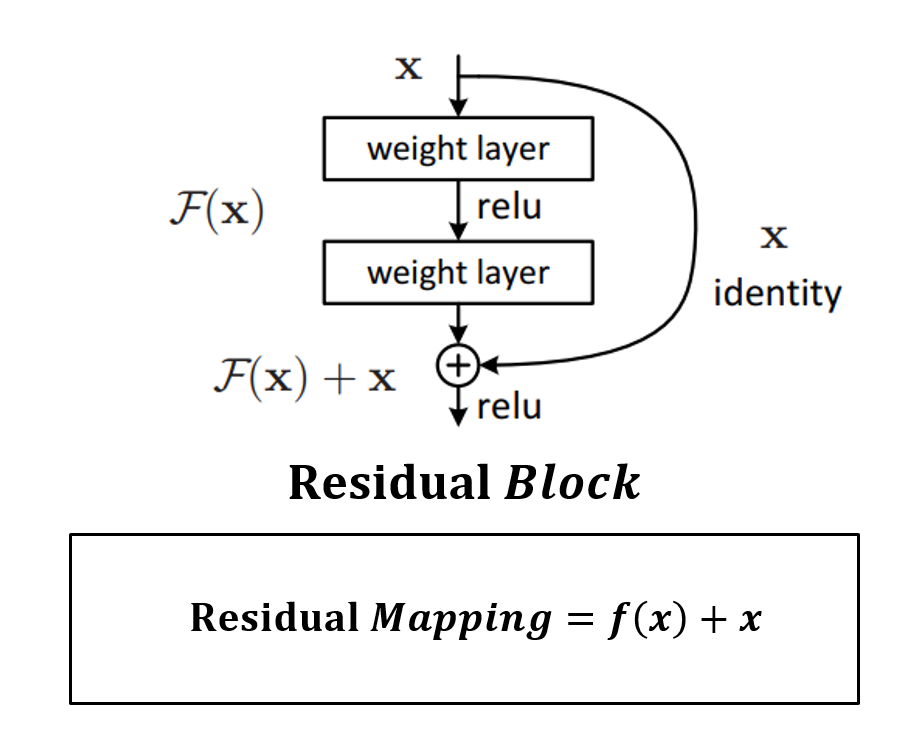
Residual Block

F(x) : weight layer => relu => weight layer 

x : identity

 

 weight layer들을 통과한 F(x)와 weight layer들을 통과하지 않은 x의 합을 Residual Mapping 이라 하고, 그림의 구조를 Residual Block이라 하고, Residual Block이 쌓이면 Residual  Network(ResNet)이라고 한다.

 

 Residual Mapping은 간단하지만, Overfitting, Vanishing Gradient 문제가 해결되어 성능이 향상됐었다.

이 벡터들과 layer-normalization 과정을 시각화해보면 다음과 같다.

이것은 Decoder 내에 있는 sub-layer 들에도 똑같이 적용되어 있다.

 

 6. Position-wise Feed Foward Networks

 모든 Encoder와 Decoder층에 Position-wise Feed-Forward Network가 존재한다. 이 층에서는 2번의 Linear transformation을 수행하고, 두 Linear transformation 사이에는 ReLU 연산을 수행한다.

 같은 Encoder, Decoder block 내에서는 동일한 Feed-Forward Network이다. (seperately and identically)

- Decoder 

1. embedding

 Decoding은 Decoder가 출력을 완료했다는 special 기호인 <end of sentence> (<eos>)를 출력할 때까지 반복된다. 각 스텝마다의 출력된 단어는 다음 스텝의 가장 밑단의 Decoder에 들어가고 Encoder와 마찬가지로 여러 개의 Decoder를 거쳐 올라간다. Encoder와는 다르게 입력값이 순차적으로 들어가게 된다. 또한, Encoder의 입력에 했던 것과 동일하게 embedding 한 후 Positional Encoding을 추가하여 Decoder에게 각 단어의 위치 정보를 더해준다.

 

2. Masked Multi-Head Attention

 기존의 Encoder-Decoder 구조의 모델들은 입력값을 순차적으로 전달받으므로 다음 시점 t+1을 예측할 때 이용가능한 입력값이 현재 시점 t로 한정된다. 하지만 Transformer는 입력값을 순차적으로 받는 것이 아닌 전체 입력값을 한번에 받기 때문에 다음시점 t+1을 예측할 때 이미 다음시점에 대한 입력값까지 받아볼 수 있다는 문제가 발생한다. 이러한 문제를 해결하기 위해 등장한 mechanism이 Look-ahead Mask라고 한다. 이 방법을 이용한 Attention을 Masked Attention이라고 한다.

다음은 실제 적용된 예시이다.

 

4개의 입력값을 받았을 때 Self-Attention Value를 계산하는 과정을 생각해보자.

 

 Attention Score의 행렬 (i, j) 원소는 i번째 입력값(Query)와 j번째 입력값(Key, Value)사이의 유사도를 의미한다. 입력값이 순서를 가진 경우 i번째 입력값은 1, 2, 3, ..., i 까지의 값을 활용할 수 있기 때문에 행렬이 윗대각 원소들은 주어진 입력값이 볼 수 없는 미래 시점의 입력값과의 유사도이다. 따라서 해당 부분을 이용한다면 위에서 언급한 문제가 발생하는 것이다.

 

  이 문제를 해결하기위해 Attention Score를 계산할 때 i ≥ j인 원소만 이용할 수 있도록 Transformer에서는 윗대각 원소들을 -inf 로 변경하는 Look-ahead Mask mechnism을 이용한다. 여기에 Softmax를 취해 Attention weight들을 0으로 만들어준다. 

 

3. Encoder-Decoder Attention

Masked Self-Attention 이후에 나오는 Encoder-Decoder Attention은 Encoder의 출력값과 Decoder의 입력값을 이용하는 Attention 이다. 시점 t에서 예측에 도움이 되는 Encoder의 출력값들만 이용하고자 하는 것이 목적이므로 Encoder의 출력값이 Key와 Value를 이루고,  Query는 Decoder의 Masked Self-Attention을 거친 입력값이 된다.

 

 4. Final Linear and Softmax Layer

 여러 개의 Decoder를 거치고 나면 벡터 하나가 출력된다. 어떻게 이 하나의 벡터를 단어로 바꿀 수 있을까? 이것이 바로 마지막에 있는 Linear layer 과 Softmax layer가 하는 일이다.

 Linear layer은 Fully Connected Neural Network으로 Decoder가 마지막으로 출력한 벡터를 단어의 사이즈(vocabulary size) 만큼의 벡터인 logits 벡터로 투영시킨다.

 예를 들어, 우리의 모델이 Train 데이터에서 총 10,000개의 영어 단어를 학습하였다고 가정해보면 이 경우 logits vector의 크기는 10,000이 될 것이다. 이 logits vector의 각 셀은 그에 대응하는 각 단어에 대한 점수가 된다. 이렇게 되면 우리는 Linear layer의 결과로서 나오는 출력에 대해서 해석을 할 수 있게 된다.

  다음에 나오는 Softmax layer는 이 점수들을 확률로 변환해주는 역할을 한다. 셀들의 변환된 확률 값들은 모두 양수 값을 가지며 다 더하게 되면 1이 된다. 가장 높은 확률 값을 가지는 셀에 해당하는 단어가 해당 스텝의 최종 결과물로서 출력된다.

 

 위의 그림에 나타나 있는 것과 같이 Decoder에서 나온 출력은 Linear layer 와 Softmax layer를 통과하여 최종 출력 단어로 변환된다.

 

💡학습 세부사항

1. 데이터셋 : WMT 2014 English-German dataset (4.5million sent. pairs, byte-pair encoding), WMT 2014 English-French dataset (36M sent., 32000 word-piece vocab.)
2. 하드웨어 정보 : 8개의 NVIDIA P100 GPU를 사용해서 base model은 100,000 step (1step = 0.4초), big model 은 300,000step(1step = 1.0초) 동안 학습을 진행했다.
3. Optimizer : Adam optimizer 사용해서 learning rate는 아래와 같은 식으로, warmup step = 4000으로 두고 학습을 진행했다.
4. Residual Dropout : 각 sub-layer의 결과에 대해서 residual connection을 수행하기 전에 dropout 을 적용한다. P_drop=1 으로 지정한다. 
5. Label Smoothing : label smoothing value = 0.1로 지정해서 사용한다. Perplexity 에는 부정적인 영향을 주지만, accuracy와 BLEU 점수에는 긍정적인 영향을 준다.

 

💡실험 결과

 위는 WMT 2014 English-German translation task(EN-DE) 와 WMT 2014 English-Frensh translation task(EN-FR) 의 결과다. SOTA를 뛰어 넘을 정도의 우수한 성능을 보인다.

 

💡모델 변형

 위에서 제안한 Transformer의 구조에서 몇 가지 요소들을 변경한 후 English-German translation task에 적용한 실험 결과이다.

• (A) : head의 개수, dk.dv 값 변경한 경우 : head가 너무 많으면 오히려 성능이 떨어진다.
• (B) : dk만 변경
• (C) : 모델의 크기를 키운 경우 : 모델이 커지면 성능이 더 좋아진다.
• (D) : dropout 의 영향 : dropout 도 성능에 영향을 미친다.
• (E) : Positional embedding의 중요성 : learned positional embedding을 사용해도 성능에 큰 변화는 없다. 

 다른 task에 대한 실험 : 다른 task에 대해서도 사용이 가능할지 실험하기 위해, English Constituency Parsing task에 transformer를 적용해봤다. 최고의 성능을 제공하지는 못하지만, 의외로 상당히 좋은 성능을 제공한다는 것을 확인할 수 있다. 

 

🔥후기

너무 좋은 자료가 널려있어서 정리하기에 한결 수월했음

사실 연구실 출근 첫날이라 겁나 집중해서 공부하며 써내려왔더니 뭔가 Transformer를 알 것 같은 느낌?!

 

중간에 big O, small o 나오는 부분이 있는데 이거 통계수학 시간에 배웠었는데 역시 재수강해도 비제로받는 이유가 있구나 -> 더 공부해보고 내용추가하기

 

구현 필수.

 

앞으로 BERT에 대해서 읽어봐야겠다. 또는 Transformer가 시계열 쪽에는 어떻게 적용됐는지에 대한 논문을 읽을 수도?

 

나름 요즘 시간이 잘가는 것을 보아하니 재밌는 것 같다(?)

 

 앞서 seq2seq이나 Attention 논문 읽을 때 보다 확실히 내용적으로 어렵기도 했고 중요한 모델인것을 알고 들어가니 더 자세히 읽어야겠다는 생각에 오랜시간 투자했다.