Entropy의 정의
확률변수 X가 이산확률변수이고 그 확률밀도함수가 다음과 같이 주어져있다고 하자.
그러면 X의 엔트로피인 H(X)는 다음과 같이 정의된다.
여기서 log는 밑이 2인 로그이고, 0log0 = 0이다. (컴퓨터의 언어가 이진법이기 때문)
(참고) 0log0 = 0인 이유?




이렇게 엔트로피를 식으로 정립한 것이 바로 Claude Shannon이다. Shannon은 이 불확실성의 측정을 ‘Entropy‘라고 불렀다. 이를 H(X)라고 표시하였고 단위를 bit라고 하였다.
톺아보기
예를 들어 문자열을 출력하는 2개의 기계 X와 Y가 있다고 하자.
기계 X는
- A, B, C, D를 각각 0.25의 확률로 출력 (동일한 확률)
기계 Y는
- A : 0.5
- B: 0.125
- C: 0.125
- D: 0.25
의 확률로 출력한다.
두 기계가 출력하는 문자를 알아보기 위해 다음과 같은 전략을 사용한다.

기계 X가 출력하는 문자 1개를 구분하기 위해서 해야하는 최소 질문의 개수는 위의 그림에서 알 수 있듯이 2개이다. 하지만 기계 Y는 다르다.
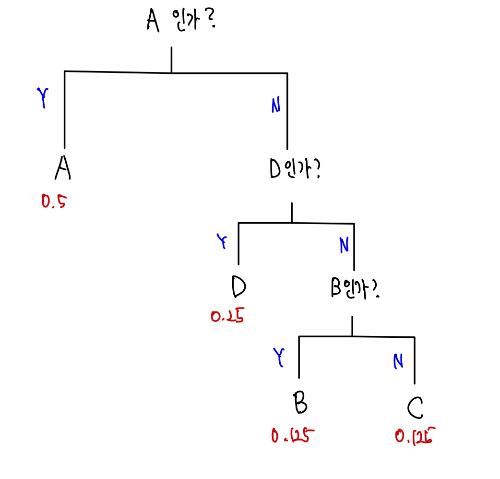
기계 Y의 경우에는 처음 질문이 (A, B) 중에 있니 (C, D) 중에 있니 전략을 쓰는 것이 비효율적이다. 왜냐하면 이미 A가 0.5의 확률로 나타나기 때문이다. 그러므로 A니 (B, C, D) 중에 있니 라고 묻는 게 더 효율적일 것이다. 또 (B,C,D) 중에서는 0.5의 확률 중에서 D가 0.25를 차지하고 있으므로 (D)니 아니면 (B,C) 중에 있니 라고 물으면 된다.
이때 기계 Y의 겨우에 최소 질문의 개수는 A가 나타날 확률에 A를 추려내기 위한 질문 개수(처음 1개의 질문만으로 A를 추려내기 가능)를 곱한다. 마찬가지로 B가 나타날 확률에 B를 추려내기 위한 질문 개수(3번의 질문으로 추려내기 가능)를 곱하고 나머지 C,D에 대해서도 똑같이 하면 된다. 이를 식으로 나타내보면
각 확률에 곱한 질문 개수를 다시 생각해보면 각 사건의 발생 확률과 연관이 있다.
이렇게 보면 위에 써놓고 본 식이 처음에 정의한 엔트로피과 같다는 것을 알 수 있다.
돌아와서, 기계 Y로 부터 1개의 문자를 맞히기 위해서는 평균 1.75개의 질문을 하면 될것이다. 만약 우리가 100개의 문자를 맞추고 싶다면 기계 X에는 약 200번, 기계 Y에는 약 175번의 질문을 해야한다는 것을 뜻한다. 이는 기계 Y가 기계 X보다 더 적은 정보량을 생산한다고 볼 수 있다. 왜냐하면 기계 Y의 불확실성이 더 적기 때문이다. 다시 말해, 모든 사건이 같은 확률로 일어나는 것이 가장 불확실한 것이다.
따라서 Entropy 는 가능한 모든 사건이 같은 확률로 일어날 때 그 최댓값을 갖는다. 그 각각의 확률이 모두 동등한 상황에서 조금만 벗어나도 Entropy 는 감소한다.
아래 두 경우를 고려해보자. X의 범위에 걸쳐 특정 값들만 높은 왼쪽 분포가 값들끼리 서로 비슷비슷한 오른쪽 분포보다 Entropy가 작다.
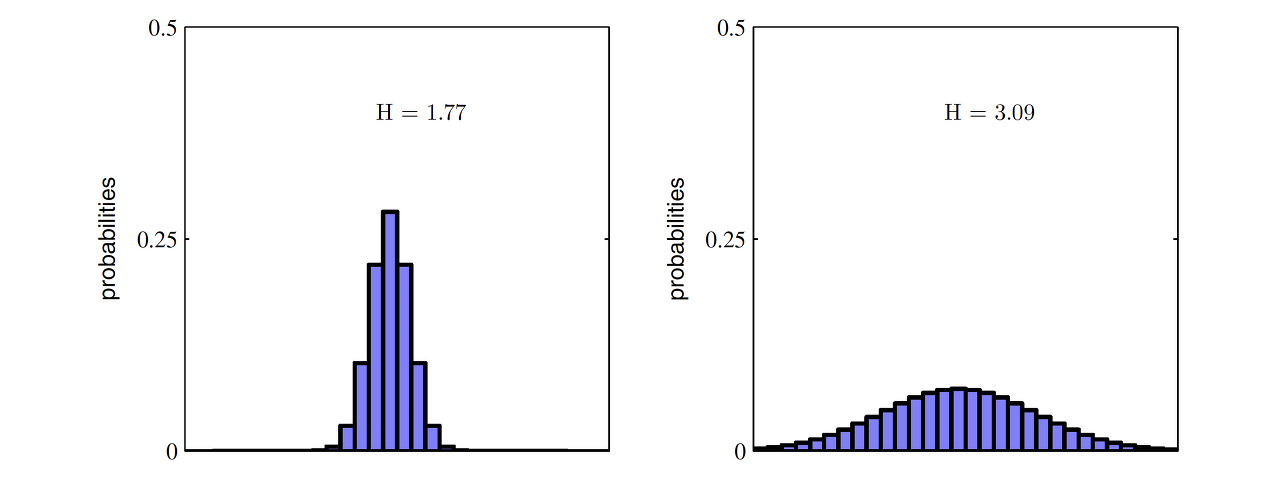
정리하자면, Entropy란 최적의 전략 하에서 그 사건을 예측하는 데에 필요한 질문 개수를 의미한다. 다른 표현으로는 최적의 전략 하에서 필요한 질문개수에 대한 기댓값으로 이해할 수 있다. 따라서, Entropy가 감소한다는 것은 우리가 그 사건을 맞히기 위해서 필요한 질문의 개수가 줄어드는 것을 의미한다. 질문의 개수가 줄어든다는 사실은 정보량도 줄어든다는 것을 뜻한다.
Cover와 Thomas의 저서 [Elements of Information Theory] 예시
Example) Let
Then,
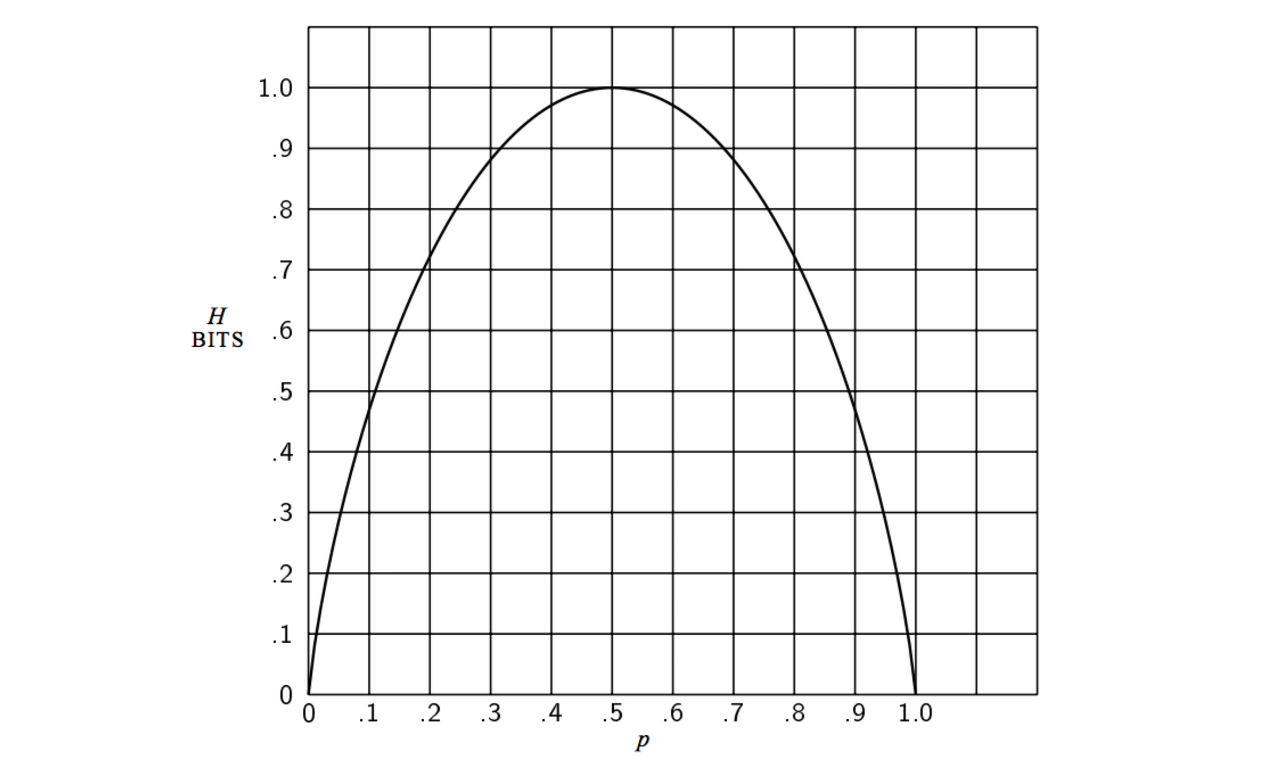
In particular, H(X) = 1 when p = 0.5, and H(X) = 0 when p = 0 or 1.
Example) Let
The entropy of X is
The game of twenty questions (스무고개 게임):
An efficient first question is "Is X = a?"
The second question is "Is X = b?"
The third question can be "Is X = c?" (or "X = d?")
The expected number of binary questions required is
Example) Suppose that we have a horse race with eight horses taking part. Assume that the probabilities of winning for the eight horses are
The entropy of horse race is
'Mathematics > Information Theory' 카테고리의 다른 글
| [Information theory] KL-divergence (0) | 2023.11.07 |
|---|---|
| [Information Theory] Cross-Entropy 톺아보기 (1) | 2023.10.05 |














