[Information theory] KL-divergence

지난 피드에서 살펴봤던 cross entropy, H(p,q) 에 이어서 이번 글에서는 KL-divergence에 대해 살펴보자.

 

단어자체가 굉장히 어려워 보여서 그렇지 이번 글을 통해서 KL-divergence가 전혀 낯선 개념이 아니라는 것을 볼 수 있다.

 

Kullback-Leibler divergence

풀네임은 쿨백-라이블러 divergence(발산), 줄여서 KL-divergence라고 부른다.

 

쿨백-라이블러 발산(Kullback–Leibler divergence, KLD)은 두 확률분포의 차이를 계산하는 데에 사용하는 함수로, 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다. 상대 엔트로피(relative entropy), 정보 획득량(information gain), 인포메이션 다이버전스(information divergence)라고도 한다.

 

출처 : Wikipedia

 

 두 확률분포의 차이를 계산한다고 나와있는데, 두 분포의 무엇의 차이를 계산하는 것일까? 바로 엔트로피를 계산하는 것이다. 앞서 두 분포가 관여하는 개념이었던 Cross-Entropy를 떠올려보자. Cross-Entropy로부터 KL-divergence가 무엇인지 수식으로 유도해보도록 하겠다.

 

 

 H(p,q)를 전개해보면 그 안에 이미 확률분포 p의 엔트로피 H(p) 가 들어있다.  H(p) 에 무언가 더해진 결과가 바로 Cross-Entropy이다. 이때 이 무언가 더해지는 것이 바로 “정보량 차이” 인데, 이 정보량 차이가 바로 KL-divergence이다. 직관적으로 정리를 해보면, KL-divergence는 p와 q의 Cross-Entropy에서 p의 엔트로피를 뺀 값이 된다. 이는 결과적으로 두 분포의 차이를 나타내는 것을 뜻한다.

 

 

KL-divergence의 정확한 식은 

 

 

 우리가 대개 Cross-Entropy를 최소화하는 것은, H(p)는 고정된 상수값이기 때문에 결과적으로는 KL-divergence를 최소화하는 것과 같다.

 

KL-divergence의 특성

KL-divergence의 대표적인 특징  2가지를 소개해보겠다.

 

0 이상이다

우선 직관적으로 생각해보면 당연히 0이상일 수밖에 없습니다. 왜냐하면 KL-divergence는 Cross-entropy에서 entropy를 뺀 값이기 때문입니다. Cross entropy는 아무리 낮아져봤자 entropy가 lower bound입니다. \H(p,q)는 q가 p가 될 때 그 최솟값을 가진다는 사실을 떠올리면 됩니다. 그러므로 \H(p,q)−H(p)\는 아무리 작아봤자 0입니다. 이런 직관적 방법도 있지만 대개 KL-divergence가 0이상이라는 사실을 증명할 때는 Jensen’s Inequality(젠슨 부등식)을 사용합니다.

 

Jensen’s Inequality

 

Convex function

 

이 부등식을 사용하려면 우선 convex function, 소위 말하는 아래로 볼록한 함수를 엄밀하게 정의해보자.

 

 

확률론 맥락에서는 X가 random variable이고, f가 convex function일 때, 이렇게 표현한다.

 

 

 

이제 KL-divergence에 관련해서 증명을 해보자.

 

 

 

따라서 KL-divergence은 non-negative의 특성을 가진다.

 

거리 개념이 아니다

 

KL-divergence를 검색해보면 알겠지만 가장 많이 나오는 특징은 바로 “KL-divergence는 거리 개념이 아니다!” 이다. 그러면서 대개 뒤따라오는 말은 “KL-divergence는 asymmetric하다”이다. 무엇이 비대칭적이냐면 KL-divergence에서 p와 q를 바꾼 값과 원래의 값이 다르다는 점이 비대칭적인 것이다. 대칭적이라면 결과값이 같아야 한다. 그 이유는 KL-divergence의 식을 살펴보면 쉽게 알 수 있다.

 

 

 

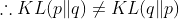
 만약에 두 확률분포 사이의 거리라면 p에서 q사이의 거리나 q에서 p사이의 거리나 같아야 한다. 하지만 KL-divergence는 그렇지 않다. 이런 이유 때문에 KL-divergence는 거리 개념(distance metric)이 아니라고 하는 것인데, 거리 개념처럼 쓸 수 있는 방법이 존재한다. 바로 Jensen-Shannon divergence이다.

 

Jensen-Shannon divergence

 

 

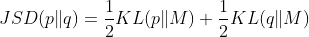
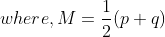
 방법은 매우 간단하다. KL-divergence를 2가지를 구하고는 평균을 내는 방식인데, 이렇게 간편하게 쓸 수 있지만 Jensen-Shannon divergence는 KL-divergence만큼 자주 쓰이지 않는다.

 

KL-divergence와 log likelihood

 

- 전체를 알 수 없는 분포 p(x)에서 추출되는 데이터를 우리가 모델링하고 싶다고 가정해보자.

- 이 분포에 대해 어떤 학습 가능한 parameter θ의 parametric distribution q(x|θ)를 이용해 근사시킨다고 가정해보자.

 

 이 θ를 결정하는 방법 중 하나는 바로 p(x)와 q(x|θ) 사이의 KL-divergence 를 최소화시키는 θ를 찾는 것이다. 우리가 p(x) 자체를 모르기 때문에 이는 직접 해내기는 불가능하다. 하지만 우리는 이 p(x)에서 추출된 몇 개의 샘플 데이터는 알 수 있다. 따라서 p(x)에 대한 기댓값은 그 샘플들의 평균을 통해 구할 수 있게 된다.

 

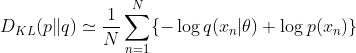
 log(x_n)은 θ에 대해 독립이고, −log q(x_n|θ) 는 training set으로 얻은 q(X|θ) 분포 하에서 θ 에 대한 negative log likelihood 이다. 그러므로 KL-divergence를 minimize하는 것이 likelihood를 maximize하는 것과 같다는 것을 알 수 있다.

 

정리

Cross entropy는 negative log likelihood와 같다. 그래서 cross entropy를 minimize하는 것이 log likelihood를 maximize하는 것과 같다. 그리고 확률분포 p,q​에 대한 cross entropy는 H(p)+KL(p|q)​이므로 KL-divergence를 minimize하는 것 또한 결국 log likelihood를 maximize하는 것과 같게 된다.